题目内容
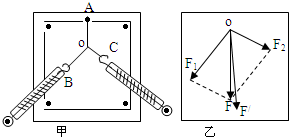
3．
质量为m1的小环A套在光滑的直角杆上，MN部分竖直，小 环A与物块B用细绳连接，如图所示．物块B的质量为m2，小环A在M点由静止释放，M、N间距为h，ON水平，OM与竖直方向的夹角为θ，则（ ）| A． | 小环A运动到N点时，小环A的速度为零 | |
| B． | 小环A运动到N点时，物块B的速度最大 | |
| C． | 小环A从M点运动到N点的过程中，小环A一直做加速运动 | |
| D． | 小环A从M点运动到N点的过程中，绳的拉力对A做的功为$\frac{{m}_{2}gh（1-sinθ）}{cosθ}$ |
分析 物体A到达N点时，对物体的速度正交分解即可求的速度，再以AB为整体由动能定理即可求的速度，再以A为动能定理求的拉力做功
解答 解：A、小环A到达N点时由速度的合成与分解可知
，v1不为零，v2为零即B的速度为零，故AB错误；
C、对m1受力分析可知绳对物体A由拉力，但与竖直方向的夹角增大，故到达N点 时绳的拉力在竖直方向分力为零，故加速度向下，故小环A不可能一直加速度，故C错误
D、由图中几何关系可得：$MO=\frac{h}{cosθ}$，NO=htanθ
以AB为整体，由动能定理可知：$-{m}_{1}gh+{m}_{2}gh（\frac{1}{cosθ}-tanθ）=\frac{1}{2}{m}_{1}{v}^{2}$
v=$\sqrt{\frac{2[{m}_{2}（1-sinθ）-{m}_{1}cosθ]gh}{{m}_{1}cosθ}}$
对A有动能定理可知：W-m1gh=$\frac{1}{2}{m}_{1}{v}^{2}$-0，
代入解得：W=$\frac{{m}_{2}gh（1-sinθ）}{cosθ}$，故D正确；
故选：D
点评 分析多个物体的受力时，一般先用整体法，再用隔离法分析单个物体的受力，利用动能定理即可求的，本题就是典型的应用整体隔离法的题目
练习册系列答案
53随堂测系列答案
相关题目
3．下列说法正确的是（ ）
| A． | 温度、压力，电磁作用可以改变液晶的光学性质 | |
| B． | 改进内燃机结构，提高内燃机内能转化率，最终可能实现内能完全转化为机械能 | |
| C． | 分子a从远处靠近固定不动的分子b，当a只在b的分子力作用下到达所受的分子力为零的位置时，a的动能一定最大 | |
| D． | 气体温度每升高1K所吸收的热量与气体经历的过程有关 | |
| E． | 大颗粒的盐磨成了细盐，就变成了非晶体 |
14．
如图，有一矩形线圈，面积为S，匝数为N，内阻为r，绕OO′轴以角速度ω做匀速转动，当它从如图所示位置转过90°的过程中，下列说法中正确的是（ ）
如图，有一矩形线圈，面积为S，匝数为N，内阻为r，绕OO′轴以角速度ω做匀速转动，当它从如图所示位置转过90°的过程中，下列说法中正确的是（ ）| A． | 线圈中电流的有效值为$\frac{NBSω}{（R+r）}$ | |
| B． | 通过电阻的电荷量为$\frac{NBS}{（R+r）}$ | |
| C． | 电阻两端的电压值为$\frac{NBSωR}{（R+r）}$ | |
| D． | 在电阻R上产生的热功率为$\frac{{N}^{2}{B}^{2}{S}^{2}{ω}^{2}}{（R+r）}$ |
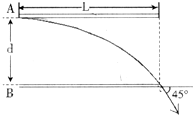如图所示为一带电的平行板电容器（电容器内部的电场可视为竖直方向的匀强电场，板外电场忽略不计）．一带电粒子以某一水平速度沿A板边缘垂直于电场线方向射入，离开电场时，它刚好贴着下板边缘飞出，其速度与水平方向成45°角．已知电容器两极板长为L，粒子所受的重力忽略不计．求：
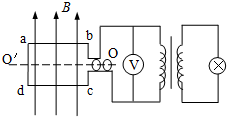一矩形线框abcd，电阻不计，ab=1m，bc=0.5m，将其置于匀强磁场中，磁场的磁感应强度B=6T，线框与理想变压器原线圈连接，变压器原副线圈的匝数比为100：1，副线圈两端接入一只标有“3V、1.5W”的小灯泡，如图所示，当abcd线框绕竖直轴OO′匀速转动时，小灯泡恰好正常发光，求：
12．当重力对物体做正功时，关于物体重力势能和动能的变化情况，下面说法正确的是（ ）
| A． | 重力势能一定增加，动能可能减小 | B． | 重力势能一定减小，动能可能不变 | ||
| C． | 重力势能一定减小，动能一定增加 | D． | 重力势能可能不变，动能一定增加 |