题目内容
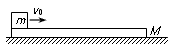
如图所示，物块质量m=0.5kg（可看作质点），它与木板之间动摩擦因数μ1=0.5．长L=3m、质量M=2kg的木板，静止于粗糙水平地面上，木板与水平地面间的动摩擦因数μ2=0.02．现给物块一个初速度v0，使物块从木板的左端滑上木板，物块刚好不会从木板上滑下．g取10m/s2，求：（1）物块与木板间相对运动的过程中，物块加速度a1的大小及木板加速度a2的大小
（2）物块的初速度v0．
（3）整个运动过程中水平地面对木板的摩擦力所做的功．
分析：（1）根据牛顿第二定律求出木板的加速度以及物块的加速度．
（2）木板先做匀加速直线运动，然后做匀减速直线运动，根据牛顿第二定律，结合两者位移之差等于板长求出．
（3）先求出二者相对静止时两者的共同速度，然后根据牛顿第二定律求出木板与木块共同运动的加速度，再根据位移公式求得共同滑行的位移，然后根据动能定理求整个过程中摩擦力做的功．
（2）木板先做匀加速直线运动，然后做匀减速直线运动，根据牛顿第二定律，结合两者位移之差等于板长求出．
（3）先求出二者相对静止时两者的共同速度，然后根据牛顿第二定律求出木板与木块共同运动的加速度，再根据位移公式求得共同滑行的位移，然后根据动能定理求整个过程中摩擦力做的功．
解答：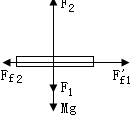
解：（1）以物块为研究对象，根据牛顿第二定律可得：
Ff1=μ2mg=ma1
代入数据解得：a1=5m/s2
以木板为研究对象，受力如图．
竖直方向合力为零，可得：F2=F1+Mg
又有Ff2=μ1F2
根据牛顿第二定律得：Ff1-Ff2=Ma2
代入数据解得：a2=1m/s2
（2）当物块滑到木板右端时，两者恰好有共同速度．设运动时间为t1，物块和木板运动的位移分别为s1、s2
根据题意得：v0-a1t1=a2t1 s1-s2=L
s1=v0t1-
a1t12 s2=
a2t12
代入数据解得：v0=6m/s
（3）物块相对于木板不滑动时，两者的共同速度为v，
则 v=a2t1=1m/s2
设物块与木板共同运动的加速度为a，
对整体由牛顿第二定律得：μ1（M+m）g=（M+m）a
代入数据解得：a=μ1g=0.2m/s2
共同滑行的位移s=
=2.5m
由s2=
a2t12解得s2=0.5m
整个运动过程中水平地面对木板的摩擦力所做的功
W=-Ff2（s+s2）=-μ1（M+m）g（s+s2）
解得：W=-1.5J
答：（1）物块与木板间相对运动的过程中，物块加速度a1的大小为5m/s2木板加速度a2的大小为1m/s2
（2）物块的初速度v0为6m/s．
（3）整个运动过程中水平地面对木板的摩擦力所做的功为-1.5J．
解：（1）以物块为研究对象，根据牛顿第二定律可得：Ff1=μ2mg=ma1
代入数据解得：a1=5m/s2
以木板为研究对象，受力如图．
竖直方向合力为零，可得：F2=F1+Mg
又有Ff2=μ1F2
根据牛顿第二定律得：Ff1-Ff2=Ma2
代入数据解得：a2=1m/s2
（2）当物块滑到木板右端时，两者恰好有共同速度．设运动时间为t1，物块和木板运动的位移分别为s1、s2
根据题意得：v0-a1t1=a2t1 s1-s2=L
s1=v0t1-
| 1 |
| 2 |
| 1 |
| 2 |
代入数据解得：v0=6m/s
（3）物块相对于木板不滑动时，两者的共同速度为v，
则 v=a2t1=1m/s2
设物块与木板共同运动的加速度为a，
对整体由牛顿第二定律得：μ1（M+m）g=（M+m）a
代入数据解得：a=μ1g=0.2m/s2
共同滑行的位移s=
| v2 |
| 2a |
由s2=
| 1 |
| 2 |
整个运动过程中水平地面对木板的摩擦力所做的功
W=-Ff2（s+s2）=-μ1（M+m）g（s+s2）
解得：W=-1.5J
答：（1）物块与木板间相对运动的过程中，物块加速度a1的大小为5m/s2木板加速度a2的大小为1m/s2
（2）物块的初速度v0为6m/s．
（3）整个运动过程中水平地面对木板的摩擦力所做的功为-1.5J．
点评：本题综合考查了牛顿第二定律和运动学公式，知道加速度是联系力学和运动学的桥梁．对于第三问抓住临界情况，结合牛顿第二定律求解
练习册系列答案
相关题目
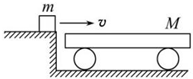如图所示，物块质量m=4kg，以速度v=2m/s水平滑上一静止的平板车，平板车质量M=16kg，物块与平板车之间的动摩擦因数μ=0.2，其他摩擦不计（g=10m/s2），求：
（2）物块的初速度v0。
（2）物块的初速度v0。