题目内容
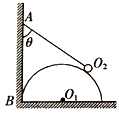
【题目】如图所示，竖直墙壁与光滑水平地面交于B点，质量为m1的光滑半圆柱体O1紧靠竖直墙壁置于水平地面上，质量为m2的均匀小球O2用长度等于A、B两点间距离l的细线悬挂于竖直墙壁上的A点，小球O2静置于半圆柱体O1上，当半圆柱体质量不变而半径不同时，细线与竖直墙壁的夹角θ就会跟着发生改变。已知重力加速度为g，不计各接触面间的摩擦，则下列说法正确的是
A. 当θ=60°，半圆柱体对面的压力大小为
B. 当θ=60°，小球对半圆柱体的压力大小为
C. 改变半圆柱体的半径，半圆柱体对竖直墙壁的最大压力大小为
D. 半圆柱体的半径增大时，其对地面的压力保持不变
【答案】AC
【解析】试题分析：对均匀小球进行受力分析，求出小球受到的拉力和支持力；然后对半圆柱体进行受力分析，根据共点力的平衡条件求解桌面的支持力；以整体为研究对象，竖直方向根据共点力的平衡条件可得圆柱体对地面的压力大小。
对均匀球进行受力分析如图所示：
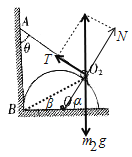
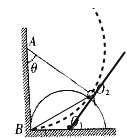
连接
和
，设
与水平面之间的夹角为
， 
与水平面之间的夹角为
；
当
时，由几何关系可知，由于
，所以
为等边三角形， 
；由圆心角与圆周角之间的关系可知
，可知小球受到的绳子的拉力T与半圆柱体对小球的支持力N相互垂直，水平方向
①，竖直方向
②，联立得
；以小球与半圆柱体组成的整体为研究对象，它们在竖直方向受到重力、地面的支持力、绳子拉力以及在水平方向受到墙对半圆柱体的弹力，竖直方向
③，所以
，根据牛顿第三定律可知，半圆柱体对地面的压力大小也为
，小球对半圆柱体的压力大小为
，A正确B错误；若改变半圆柱体的半径，当小球平衡时，小球的位置在以AB为半径的圆弧上，由几何关系可知，直线
是该圆的切线方向，所以
；则
④，以小球与半圆柱体组成的整体为研究对象，在水平方向
⑤，可知，当θ=45°时，半圆柱体受到墙对半圆柱体的弹力最大，为
，C正确；由③④可得半圆柱体在竖直方向上的受的支持力： 
⑥，由几何关系可知，增大半圆柱体的半径，则θ增大，由⑥可知，N′将增大；根据牛顿第三定律可知，半圆柱体对地面的压力将增大，D错误．
