Question

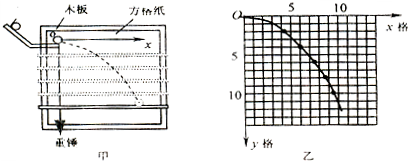
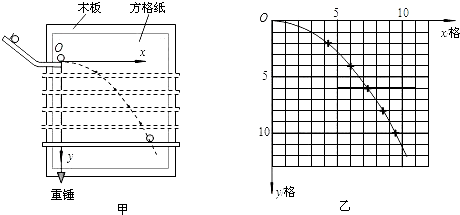
某同学在“研究平拋物体的运动”的实验中，通过描点法画出小球平拋运动的轨迹，并求出小球平拋运动的初速度．他先调整斜槽轨道使槽口末端水平，然后在方格纸上建立好直角坐标系xOy，将方格纸上的坐标原点O与轨道槽口末端重合，Oy轴与重锤线重合，Ox轴水平，如图13甲所示．实验中使小球每次都从斜槽同一高度由静止滚下，经过一段水平轨道后飞出．依次均匀下移水平挡板的位置，分别得到小球在挡板上的落点，并在方格纸上标出相应的点迹，再用平滑曲线将方格纸上的点迹连成小球的运动轨迹，如图13乙所示．已知方格边长L=5cm，重力加速度g=10m/s²．则小球平拋的初速度v₀=

1.5

m/s．（结果保留两位有效数字）

Answer 1

分析：小球离开导轨后做平抛运动，将平抛运动分解为水平方向的匀速直线运动和竖直方向的自由落体运动，据此列方程即可求解

解答：解：从轨迹图上取距O较远的任一点，例如点（6，4），即x=0.3 m，y=0.2 m，
而x=v₀t，y=

1

2

gt²，
解得：v₀=1.5 m/s．
故答案为：1.5

点评：本题主要考查了平抛运动规律的理解和应用，平时要加强练习，提高应用基本规律解决问题能力，难度不大，属于基础题．