��Ŀ����
12��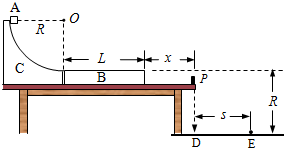 ��ͼ��ʾ���⻬��$\frac{1}{4}$Բ������̶��������ϣ�����ΪM�ij�ľ��B����Բ�������ֹ�ڹ⻬ˮƽ�����ϣ���ľ����ϱ�����Բ������ĵ����ߴ���ͬһˮƽ�棬������Ҷ˹̶�һ��С�ɺ��Ե�С����P���ֽ�����Ϊm��С���A��Բ������Ķ����ɾ�ֹ�ͷţ���֪M=2m��Բ������İ뾶ΪR����ľ����ϱ��������ĸ߶�ΪR��A��B��Ķ�Ħ��������=0.5���������ٶ�Ϊg������B�ij���ΪL��P��B�Ҷ˵ľ���Ϊx������
��ͼ��ʾ���⻬��$\frac{1}{4}$Բ������̶��������ϣ�����ΪM�ij�ľ��B����Բ�������ֹ�ڹ⻬ˮƽ�����ϣ���ľ����ϱ�����Բ������ĵ����ߴ���ͬһˮƽ�棬������Ҷ˹̶�һ��С�ɺ��Ե�С����P���ֽ�����Ϊm��С���A��Բ������Ķ����ɾ�ֹ�ͷţ���֪M=2m��Բ������İ뾶ΪR����ľ����ϱ��������ĸ߶�ΪR��A��B��Ķ�Ħ��������=0.5���������ٶ�Ϊg������B�ij���ΪL��P��B�Ҷ˵ľ���Ϊx��������1��С���A����Բ�������ʱ�Թ����ѹ����
��2����B��P������ײʱA��Bǡ�ù��٣���L��xӦ����ʲô������
��3����L=$\frac{3}{2}$R��B��P��ײ��ֹ��A����B���䵽ˮƽ�����ϵ�E�㣬�Է�������xȡ��ֵͬʱ��E���������Ҷ˵�ˮƽ���� s��x�кι�ϵ��
���� ��1��A�ɾ�ֹ�����˹����У����ݶ��ܶ����������Ͷ˵��ٶȣ�����͵㣬������������ʽ��ʽ������⣻
��2��B��P��ײʱ��A��Bǡ�ù��٣���A��λ��ΪxA��B��λ��ΪxB����ײ�����У������غ㣬���ݶ����غ㶨�ɶ�����ʽ���ٷֱ��A��B���ݶ��ܶ�����ʽ������������⣻
��3����x��xB����B��P��ײʱ��A��B�ѹ��٣����ݶ��ܶ�����ʽ���A����Bʱ���ٶȣ�A����B����ƽ���˶�������ƽ���˶�������ʽ��⣬��0��x��xB����B��P��ײʱ��A��B��δ���٣�����A������B�ϻ��У����ݶ��ܶ�����⣮
��� �⣺��1��A�ɾ�ֹ�����˹��̣�$mgR=\frac{1}{2}m{{v}_{0}}^{2}$��
��ã�${v}_{0}=\sqrt{2gR}$
A����͵�ʱ��$N-mg=m\frac{{{v}_{0}}^{2}}{R}$��
��ã�N=3mg
��ţ�ٵ������ɣ�A�Թ����ѹ����СN��=N=3mg��������ֱ���£�
��2��B��P��ײʱ��A��Bǡ�ù��٣���A��λ��ΪxA��B��λ��ΪxB������
mv0=��m+M��v����
��B��$��mg{x}_{B}=\frac{1}{2}M{{v}_{��}}^{2}$��
��A��$-��mg{x}_{A}=\frac{1}{2}M{v}_{��}^{2}-\frac{1}{2}m{v}_{0}^{2}$��
�����٢ۢܢݽ�ã�${x}_{A}=\frac{16}{9}R$��${x}_{B}=\frac{4}{9}R$
������$x={x}_{B}=\frac{4}{9}R$��$L��{x}_{A}-{x}_{B}=\frac{4}{3}R$
��3������$L=\frac{3R}{2}��\frac{4}{3}R$����B��P��ײǰ��A���Ử��B��
��i����x��xB����B��P��ײʱ��A��B�ѹ��٣���A����Bʱ���ٶ�ΪvA����������A����B�Ĺ����У�$-��mg��\frac{3}{2}R-\frac{4}{3}R��=\frac{1}{2}m{{v}_{A}}^{2}-\frac{1}{2}m{{v}_{��}}^{2}$��
�����٢ۢ�ã�${v}_{A}=\frac{\sqrt{2gR}}{6}$��
A����B����ƽ���˶������У�$R=\frac{1}{2}g{t}^{2}$��
s=vAt��
�����ߢ���ã�$s=\frac{1}{3}R$
��ii����0��x��xB����B��P��ײʱ��A��B��δ���٣�����A������B�ϻ��У�A����Bʱ���ٶ�ΪvA�����У�$-��mg��\frac{3}{2}R+x��=\frac{1}{2}m{{v}_{A}}^{2}-\frac{1}{2}m{{v}_{0}}^{2}$��
��ã�${v}_{A}=\sqrt{\frac{1}{2}g��R-2x��}$��0��˵��A�ܻ���B��
������ã�$s=\sqrt{{R}^{2}-2Rx}$
�𣺣�1��С���A����Բ�������ʱ�Թ����ѹ��Ϊ3mg��������ֱ���£�
��2����B��P������ײʱA��Bǡ�ù��٣���L��xӦ����$x=\frac{4}{9}R$��$L��\frac{4}{3}R$��
��3����x��xB��$s=\frac{1}{3}R$����0��x��xB��$s=\sqrt{{R}^{2}-2Rx}$��
���� ������Ҫ�����˶����غ㶨�ɡ����ܶ�����ƽ���˶�������ʽ�Լ���������ʽ��ֱ��Ӧ�ã��ؼ��Ƿ���������������������˶��������ѡ����ʵĶ�����⣬֪��A����B����ƽ���˶����ܷ�����������ۣ��Ѷ����У�

 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�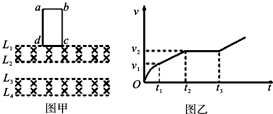 ��ͼ����ʾ������ֱ�����������������ȵ�ˮƽ����L1��L2��L3��L4����L1��L2��L3��L4֮�������ǿ�ų����Ÿ�Ӧǿ�ȴ�С��Ϊ1T������ֱ����������ƽ���������һ������Ȧabcd������cd=L=0.5m������Ϊ0.1kg������Ϊ2���������ͼʾλ�þ�ֹ�ͷţ�cd����L1�غϣ����ٶ���ʱ��ı仯��ϵ��ͼ����ʾ��t1ʱ��cd����L2�غϣ�t2ʱ��ab����L3�غϣ�t3ʱ��ab����L4�غϣ�t2��t3֮��ͼ��Ϊ��t��ƽ�е�ֱ�ߣ�t1��t2֮���t3֮���ͼ�߾�Ϊ��бֱ�ߣ���֪t1��t2��ʱ����Ϊ0.6s�������˶���������Ȧƽ��ʼ�մ�����ֱ�����������ٶ�gȡ10m/s2��������
��ͼ����ʾ������ֱ�����������������ȵ�ˮƽ����L1��L2��L3��L4����L1��L2��L3��L4֮�������ǿ�ų����Ÿ�Ӧǿ�ȴ�С��Ϊ1T������ֱ����������ƽ���������һ������Ȧabcd������cd=L=0.5m������Ϊ0.1kg������Ϊ2���������ͼʾλ�þ�ֹ�ͷţ�cd����L1�غϣ����ٶ���ʱ��ı仯��ϵ��ͼ����ʾ��t1ʱ��cd����L2�غϣ�t2ʱ��ab����L3�غϣ�t3ʱ��ab����L4�غϣ�t2��t3֮��ͼ��Ϊ��t��ƽ�е�ֱ�ߣ�t1��t2֮���t3֮���ͼ�߾�Ϊ��бֱ�ߣ���֪t1��t2��ʱ����Ϊ0.6s�������˶���������Ȧƽ��ʼ�մ�����ֱ�����������ٶ�gȡ10m/s2��������| A�� | ��0��t1ʱ���ڣ�ͨ����Ȧ�ĵ����Ϊ2.5C | |
| B�� | ��Ȧ�����˶����ٶȴ�СΪ8m/s | |
| C�� | ��Ȧ�ij���Ϊ2m | |
| D�� | 0��t3ʱ���ڣ���Ȧ����������Ϊ4.2J |
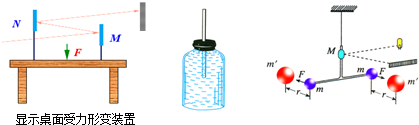
| A�� | ����˼�뷽�� | B�� | �Ŵ��˼�뷽�� | C�� | ���Ʊ����ķ��� | D�� | �����˼�뷽�� |
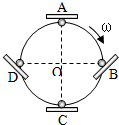 ��̫�����ǽ������ڹ�������н����е�һ�ֽ������ģ��������˶�ʱ�������߰�����վ�����ֳ�̫�����ģ����Ϸ�һ��̫���������趯����ʱ����ȴ���������ϣ��ֽ�̫�������ͼ��ʾ��ƽ���С�������Ľ�������������ֱ����ʼ�ղ�������������Բ���˶��������˶���ͼ�е�A��B��C��Dλ��ʱ�����������˶����ƣ�AΪԲ�ܵ���ߵ㣬CΪ��͵㣬B��D��Բ��O�ȸߣ����D��A���̣�������
��̫�����ǽ������ڹ�������н����е�һ�ֽ������ģ��������˶�ʱ�������߰�����վ�����ֳ�̫�����ģ����Ϸ�һ��̫���������趯����ʱ����ȴ���������ϣ��ֽ�̫�������ͼ��ʾ��ƽ���С�������Ľ�������������ֱ����ʼ�ղ�������������Բ���˶��������˶���ͼ�е�A��B��C��Dλ��ʱ�����������˶����ƣ�AΪԲ�ܵ���ߵ㣬CΪ��͵㣬B��D��Բ��O�ȸߣ����D��A���̣�������| A�� | �����߶ԡ�̫���������� | B�� | ��̫���Ļ�е���غ� | ||
| C�� | ��̫���������������� | D�� | �������ԡ�̫���������� |
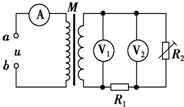 ��ͼ��ʾ��M��С�������ѹ����ԭ������Ȧ����֮��n1��n2=10��1��������a��b�����ҽ����Դ����ѹu=311sin 100��t��V������ѹ���Ҳಿ��Ϊ��ϵͳԭ��ͼ������R2Ϊ�뵼�����������ƳɵĴ���������������¶����߶���С��R1Ϊ��ֵ���裮����˵����ȷ���ǣ�������
��ͼ��ʾ��M��С�������ѹ����ԭ������Ȧ����֮��n1��n2=10��1��������a��b�����ҽ����Դ����ѹu=311sin 100��t��V������ѹ���Ҳಿ��Ϊ��ϵͳԭ��ͼ������R2Ϊ�뵼�����������ƳɵĴ���������������¶����߶���С��R1Ϊ��ֵ���裮����˵����ȷ���ǣ�������| A�� | ��ѹ��V1��ʾ��Ϊ31.1V | |
| B�� | ��ѹ������Ȧ�е�����Ƶ��Ϊ25Hz | |
| C�� | ��R2���ڴ����ֻ�ʱ����ѹ��V2��ʾ����С��������A��ʾ����� | |
| D�� | ��R2���ڴ����ֻ�ʱ����ѹ��ԭ��Ȧ�����빦�ʱ�С |
| A�� | �������о���ɼ������ʱ������ˡ��糡���ĸ��� | |
| B�� | ����������ʿ��¡�٤���ԣ����ǵѿ�����û�н������ĸ����ţ�ٵ�ΰ��֮��������������临�Ӷ���������ó���Ϊ��������Ϊ���ţ�ٵ�һ���ɶ�ȷ����һ����Ҫ���������� | |
| C�� | ���ĵ���ͨ��Ť��ʵ�����˾��������� | |
| D�� | ŷķ����I=$\frac{U}{R}$���ñ�ֵ���巨�����˵���ǿ����һ������ |
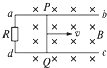 ��ͼ��ʾ���ڴŸ�Ӧǿ��B=1.0T����ǿ�ų��У�������PQ������F�������ڴֲ�U�ε��������ٶ�v=2m/s�������ٻ���������������L=1.0m������R=3.0����������PQ�ĵ���r=1.0�������������Բ��ƣ�������˵����ȷ���ǣ�������
��ͼ��ʾ���ڴŸ�Ӧǿ��B=1.0T����ǿ�ų��У�������PQ������F�������ڴֲ�U�ε��������ٶ�v=2m/s�������ٻ���������������L=1.0m������R=3.0����������PQ�ĵ���r=1.0�������������Բ��ƣ�������˵����ȷ���ǣ�������| A�� | ͨ��R�ĸ�Ӧ�����ķ���Ϊ��d��a | |
| B�� | ������PQ���˵�ѹΪ2 V | |
| C�� | ������PQ�ܵ��İ�������СΪ0.5 N | |
| D�� | ����F������С���ڵ�·�����Ľ����� |
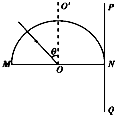 �̶��İ�Բ�β���ש�ĺ������ͼ��ʾ��O��ΪԲ�ģ�OO��Ϊֱ��MN�Ĵ��ߣ��㹻���
�̶��İ�Բ�β���ש�ĺ������ͼ��ʾ��O��ΪԲ�ģ�OO��Ϊֱ��MN�Ĵ��ߣ��㹻�������PQ��������ש�Ҳ��Ҵ�ֱ��MN����A��B���ֵ�ɫ����ɵ�һ�����ذ뾶��������O�㣬���������OO��нǦȽ�Сʱ������NQ�������������ߣ�������Ƚǣ�����=��ʱ������NQ����A��Ĺ����ʧ����������Ƚǣ�����=��ʱ������NQ����B��Ĺ����ʧ��������˵������ȷ���ǣ�������
| A�� | A����MN�淢��ȫ������ٽ�DZ�B�����MN�淢��ȫ������ٽ�Ǵ� | |
| B�� | ����ש��A��������ʱȶ�B��Ĵ� | |
| C�� | A���ڲ���ש�д����ٶȱ�B��Ĵ� | |
| D�� | �����ȣ���ʱ������PQ����2����� | |
| E�� | �£��ȣ�$\frac{��}{2}$ʱ������PQ��ֻ��1����� |
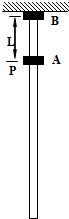 ��ͼ��ʾ��һ����ϸ���ȵij�Ϊ4Lֱ����ֱ�̶����ã���������A��B�����ɿ����ʵ��СԲ��A��B�������ֱ�ΪmA=4m��mB=m������P���Ϸ��ǹ⻬���ҳ���ΪL��P���·��Ǵֲڵģ��˶������Ļ���Ħ������С�����ڻ����Ե���������ʼ��A��ֹ��P������B�Ӹ˵Ķ����ɾ�ֹ�ͷţ�B ��A������ײ��ʱ�伫�̣�����B���ٶȷ������ϣ��ٶȴ�СΪ��ǰ��$\frac{3}{5}$����
��ͼ��ʾ��һ����ϸ���ȵij�Ϊ4Lֱ����ֱ�̶����ã���������A��B�����ɿ����ʵ��СԲ��A��B�������ֱ�ΪmA=4m��mB=m������P���Ϸ��ǹ⻬���ҳ���ΪL��P���·��Ǵֲڵģ��˶������Ļ���Ħ������С�����ڻ����Ե���������ʼ��A��ֹ��P������B�Ӹ˵Ķ����ɾ�ֹ�ͷţ�B ��A������ײ��ʱ�伫�̣�����B���ٶȷ������ϣ��ٶȴ�СΪ��ǰ��$\frac{3}{5}$����