Question

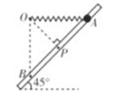
【题目】如图所示，光滑细杆AB倾斜固定，与水平方向夹角为45°，一轻质弹簧的一端固定在O点，另一端连接质量为m的小球，小球套在细杆上，O与细杆上A点等高，O与细杆AB在同一竖直平面内，OB竖直，OP垂直于AB，且，当小球位于细杆上A、P两点时，弹簧弹力大小相等。现将小球从细杆上的A点由静止释放，在小球沿细杆由A点运动到B点的过程中（已知重力加速度为g，弹簧一直处于弹性限度内且不弯曲），下列说法正确的是（　　）

A.弹簧的弹性势能先减小后增大

B.小球加速度大小等于号且方向沿杆向下的位置有三个

C.小球运动到B点时的动能为

D.小球从A点运动到P点，机械能减少了

Answer 1

【答案】BC

【解析】

根据题目中的A、P两点时，弹簧弹力相同为突破口，分析弹簧形变的变化情况，然后再结合功能关系分析。

A．由于小球在A、P两点时，弹簧弹力相同，则弹簧在OA处被拉伸，在OP处被压缩，且拉伸与压缩量相等，则在AP之间必有一个弹簧处于原长状态的位置，由对称性原理可知，在PB之间也必有一个弹簧处于原长的位置。小球在A、P、B三个位置时弹簧的弹性势能相等。在A到P的过程中，弹簧的弹性势能先减小后增大，在P到B的过程中，弹簧的弹性势能也是先减小后增大，选项A错误；

B．弹簧处于两个原长状态和小球在P点位置，小球加速度大小等于且方向沿杆向下，选项B正确；

C．小球从A点运动到B点过程中，由机械能守恒定律可得，

，

得

，

选项C正确；

D．A、P两点弹簧的弹性势能相等，因而小球在A、P两点的机械能相等，选项D错误；

故选BC。