Question

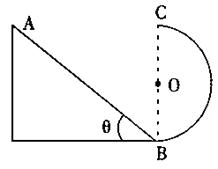
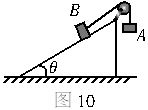
如图10所示，斜面AB与竖直半圆轨道在B点圆滑相连，斜面倾角为=45°，半圆轨道的半径为R，一小球从斜面的顶点A由静止开始下滑，进入半圆轨道，最后落到斜面上，不计一切摩擦。试求：（结果可保留根号）。

  （1）欲使小球能通过半圆轨道最高点C，落到斜面上，斜面AB的长度L至少为多大？

（2）在上述最小L的条件下，小球从A点由静止开始运动，最后落到斜面上的落点与半圆轨道直径BC的距离x为多大？

   图10

                                                     

                                                          

Answer 1

【解析】（1）由题意：小球恰好通过最高点C时，

对轨道压力N=0，此时L最小。

从A到C机械能守恒，

…                         

   （2）落到斜面上时：x=v_ct   

  解得：

【答案】（1）   （2）