题目内容
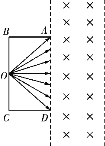
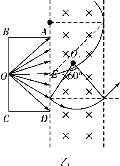
【题目】如图所示，在屏蔽装置底部中心位置O点放一医用放射源，可通过细缝沿扇形区域向外辐射速率为v的带电粒子．已知屏蔽装置宽AB为d，缝长AD为2d，粒子的质量m，电荷量为+q．若在屏蔽装置右侧条形区域内加一匀强磁场来隔离辐射，磁感应强度B，方向垂直于纸面向里，整个装置放于真空环境中．
(1)若所有的粒子均不能从条形磁场隔离区的右侧穿出，则磁场的宽度D至少是多少？
(2)若条形磁场的宽度D＝
，则射出屏蔽装置的粒子在磁场中运动的最长时间和最短时间各是多少？
【答案】(1) 
(2) 
【解析】
(1)根据
得:
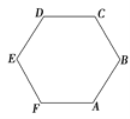
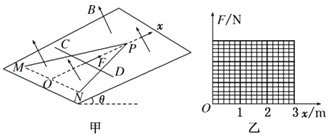
如图甲所示，根据几何关系可得，这些粒子在磁场中运动的最宽处宽度为
所以
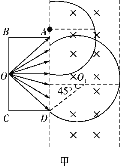
(2)根据：
得：
如图乙所示，根据几何关系可得，粒子在磁场中运动的时间最短时，弦长最短即为磁场宽度，分析可得此时圆心角
所以
当时间最长时，弧长最长，此时轨迹与右侧边界相切，由几何关系可得此时圆心角
所以
练习册系列答案
相关题目
