题目内容
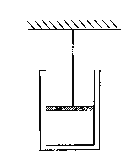
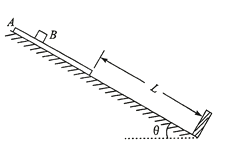
【题目】如图，倾角
的光滑斜面底端固定一块垂直于斜面的挡板。将长木板A静置于斜面上，A上放置一小物块B，初始时A下端与挡板相距L=4m，现同时无初速度释放A和B。已知在A停止运动之前B始终没有脱离A且不会与挡板碰撞，A和B的质量均为m=1kg，它们之间的动摩擦因数
，A或B与挡板每次碰撞损失的动能均为
，忽略碰撞时间，重力加速度大小
。求：
（1）A第一次与挡板碰前瞬间的速度大小v；
（2）A第一次与挡板碰撞到第二次与挡板碰撞的时间
；
（3）B相对于A滑动的可能最短时间t。
【答案】（1）
（2）
（3）
【解析】(1) B和A一起沿斜面向下运动，由机械能守恒定律有
由上式得
；
(2) 第一次碰后，对B有
故B匀速下滑
对A有：
解得：
，方向始终沿斜面向下，A将做类竖直上抛运动
设A第1次反弹的速度大小为
，由动能定理有
解得：
；
(3) 设A第2次反弹的速度大小为
，由动能定理有
解得：
即A与挡板第2次碰后停在底端，B继续匀速下滑，与挡板碰后B反弹的速度为
，加速度大小为
，由动能定理有
得B沿A向上做匀减速运动的时间
当B速度为0时，因
，故B将静止在A上
当A停止运动时，B恰好匀速滑至挡板处，B相对A运动的时间t最短，故
。
练习册系列答案
相关题目
