题目内容
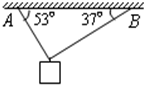
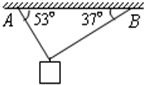如图所示，用AB两根重力不计的绳子吊起一个重物，如果每根绳所能承受的最大拉力均为2.0×103N（已知sin37°=0.6，sin53°=0.8）求：（1）当物体重力不断加大时，那根绳子将先断？
（2）物体的重力为2.0×103N时，两绳的拉力大小．
分析：（1）假设两绳均不被拉断，分析O点受力情况，由平衡条件求出当AO绳的拉力达到最大时，BO绳的拉力，判断哪个绳先断．
（2）由第1问的基础上，求得的两个绳子拉力表达式进行计算
（2）由第1问的基础上，求得的两个绳子拉力表达式进行计算
解答：解：（1）假设两绳均不被拉断．分析O点受力情况，作出力图，如图．由图看出，TBO＜TAO，说明绳子AO的拉力先达到最大值，则知AO绳先断．
（2）由几何知识：TAO=Gsin53°=1.6×103N
TOB=Gcos53°=1.2×103N
答：（1）当物体重力不断加大时，AO绳先断．
（2）物体的重力为2.0×103N时，两绳的拉力大小分别为1.6×103N，1.2×103N．
（2）由几何知识：TAO=Gsin53°=1.6×103N
TOB=Gcos53°=1.2×103N
答：（1）当物体重力不断加大时，AO绳先断．
（2）物体的重力为2.0×103N时，两绳的拉力大小分别为1.6×103N，1.2×103N．
点评：题运用假设法和图解法，比较两绳在不被拉断的情况下拉力的大小，判断哪根绳先断
练习册系列答案
教材全解字词句篇系列答案
相关题目
如图所示，水平面上两根足够长且光滑的金属导轨平行固定放置，间距为L=0.5m，一端通过导线与阻值为R=0.5Ω的电阻连接；导轨上放一金属杆ab，金属杆与导轨的电阻不计；匀强磁场的磁感强度B=1T，方向竖直向下．现用与导轨平行的恒定外力F=5N作用在金属杆上，ab杆最终将做匀速运动．
如图所示，用AB两根重力不计的绳子吊起一个重物，如果每根绳所能承受的最大拉力均为2.0×103N（已知sin37°=0.6，sin53°=0.8）求：
