题目内容
19.质量m=0.1kg的小球在细绳的拉力作用下在竖直面内做半径为r=0.2m的圆周运动,已知小球在最高点的速率为v1=2m/s,g 取10m/s2.求:(1)小球在最高点时所受拉力;
(2)小球在最高点能做圆周运动的最小速度.
分析 在最高点,根据竖直方向上的合力提供向心力求出拉力的大小,结合最高点拉力为零,根据牛顿第二定律求出最小速度.
解答 解:(1)在最高点,根据牛顿第二定律得,$mg+F=m\frac{{{v}_{1}}^{2}}{r}$,
解得F=$m\frac{{{v}_{1}}^{2}}{r}-mg=0.1×\frac{4}{0.2}-1$N=1N.
(2)根据牛顿第二定律得,mg=$m\frac{v{′}^{2}}{r}$,
解得最小速度$v′=\sqrt{gr}=\sqrt{10×0.2}m/s=\sqrt{2}m/s$.
答:(1)小球在最高点时所受拉力为1N;
(2)小球在最高点能做圆周运动的最小速度为$\sqrt{2}m/s$.
点评 解决本题的关键知道小球做圆周运动向心力的来源,知道最高点的临界情况,结合牛顿第二定律进行求解.

练习册系列答案
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
10.对万有引力定律的表达式F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$,下列说法正确的是( )
| A. | 公式中G为常量,没有单位,是人为规定的 | |
| B. | r趋向于零时,万有引力趋近于无穷大 | |
| C. | 两物体之间的万有引力总是大小相等,与m1、m2是否相等无关 | |
| D. | 两个物体间的万有引力总是大小相等,方向相反的,是一对平衡力 |
14.关于重力势能与重力做功的下列说法中正确的是( )
| A. | 重力对物体做的功等于重力势能的增加 | |
| B. | 在物体下落的过程中,如果重力做的功相等,物体所减少的重力势能一定相等 | |
| C. | 重力势能等于零的物体,不可能对别的物体做功 | |
| D. | 用手托住物体匀速上举时,手的支特力做的功等于克服重力做的功与物体所增加的重力势能之和 |
4.用一段截面半径为r、电阻率为ρ、密度为d的均匀导体材料做成一个半径为R(r<<R)的圆环.圆环落入磁感应强度为B的径向磁场中.如图所示,当圆环在加速下落时某一时刻的速度为v,则( )
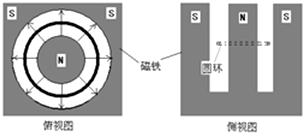

| A. | 此时整个环的电动势为E=2BvπR | |
| B. | 忽略电感的影响,此时圆环中的电流I=$\frac{Bπ{R}^{2}v}{ρ}$ | |
| C. | 此时圆环的加速度a=$\frac{{B}^{2}v}{ρd}$ | |
| D. | 如果径向磁场足够长,则圆环的最大速度vm=$\frac{2ρgd}{{B}^{2}}$ |
4.下列说法不符合物理学史实的是( )
| A. | 在研究天体运动时,牛顿提出了太阳系行星运动的三大规律 | |
| B. | 奥斯特最早发现电流周围存在磁场 | |
| C. | 在研究电磁现象时,安培引入了“场”的概念 | |
| D. | 伽利略通过理想实验,说明物体的运动不需要力来维持 |
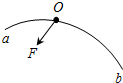
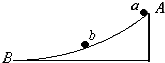 如图所示,固定圆弧轨道弧AB所含度数小于5°末端切线水平.两个相同的小球a、b分别从轨道的顶端和正中由静止开始下滑,比较它们到达轨道底端所用的时间和动能:ta=tb,Ea>2Eb(填“>”、“=”或“<”).
如图所示,固定圆弧轨道弧AB所含度数小于5°末端切线水平.两个相同的小球a、b分别从轨道的顶端和正中由静止开始下滑,比较它们到达轨道底端所用的时间和动能:ta=tb,Ea>2Eb(填“>”、“=”或“<”).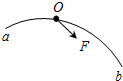
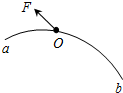

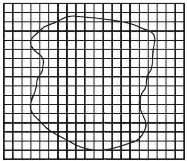 在“用油膜法估测分子的大小”的实验中,所用油酸酒精溶液的浓度为每1.0×104 mL溶液中有纯油酸6mL,用注射器测得1mL上述溶液为75滴.把1滴该溶液滴入盛水的浅盘里,待水面稳定后,将玻璃板放在浅盘上,用笔在玻璃板上描出油酸膜的形状,再把玻璃板放在坐标纸上,其形状如图所示,坐标中正方形格子的边长为1cm.则:
在“用油膜法估测分子的大小”的实验中,所用油酸酒精溶液的浓度为每1.0×104 mL溶液中有纯油酸6mL,用注射器测得1mL上述溶液为75滴.把1滴该溶液滴入盛水的浅盘里,待水面稳定后,将玻璃板放在浅盘上,用笔在玻璃板上描出油酸膜的形状,再把玻璃板放在坐标纸上,其形状如图所示,坐标中正方形格子的边长为1cm.则: