题目内容
如图1-2-2所示，半径为R的绝缘球壳上均匀地带有电荷量为+Q的电荷，另一电荷量为+q的点电荷放在球心O上，由于对称性，点电荷受力为零.现在球壳上挖去半径为r(r＜＜R)的一个小圆孔，则此时置于球心的点电荷所受力的大小为多少?方向如何?(已知静电力常量为k)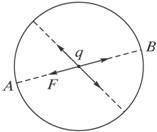
图1-2-2
思路分析：根据题目中的提示，由于对称性，点电荷受力为零，将球分割成关于球心对称的许多部分，每两对称部分对点电荷的库仑力为零.
解析：由于球壳上带电均匀，原来每条直径两端相等的一小块圆面上的电荷对球心+q的力互相平衡．现在球壳上A处挖去半径为r的小圆孔后，其他直径两端电荷对球心+q的力仍互相平衡，剩下的就是与A相对称的B处、半径也等于r的一小块圆面上电荷对它的力F，B处这一小块圆面上的电荷量为：qB=
Q=
Q.
由于半径r＜＜R，可以把它看成点电荷．根据库仑定律，它对中心+q的作用力大小为：F=k
，其方向由球心指向小孔中心．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
