题目内容
15.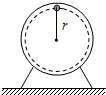 在质量为M的电动机上装有一个质量为m的转动小轮,在皮带的带动下小轮在竖直平面上做匀速圆周运动,小轮距离转轴的距离为r,在小轮转动过程中电动机刚好没有离开地面,问在整个过程中电动机对地面的最大压力.
在质量为M的电动机上装有一个质量为m的转动小轮,在皮带的带动下小轮在竖直平面上做匀速圆周运动,小轮距离转轴的距离为r,在小轮转动过程中电动机刚好没有离开地面,问在整个过程中电动机对地面的最大压力.
分析 当小轮转到最高点时,对电动机的拉力等于电动机的重力时,电动机恰好不从地面跳起,此时小轮角速度是电动机不从地面跳起时最大的线速度,以小轮为研究对象,根据牛顿第二定律求解此线速度,
当以此线速度匀速转动,小轮转到最低点时,电动机对地面的压力最大,再由牛顿运动定律求解即可.
解答 解:在小轮转动过程中电动机刚好没有离开地面,则当小轮转到最高点时,对电动机的拉力等于电动机的重力,根据牛顿第二定律得:
Mg+mg=m$\frac{{v}^{2}}{r}$…①
当以此线速度匀速转动,小轮转到最低点时,电动机对地面的压力最大,根据牛顿第二定律得:
T-mg=m$\frac{{v}^{2}}{r}$…②
由①②解得:T=Mg+2mg
对电动机受力分析,则有:
FN=Mg+T=2Mg+2mg,
根据牛顿第三定律可知,整个过程中电动机对地面的最大压力为2Mg+2mg.
答:整个过程中电动机对地面的最大压力为2Mg+2mg.
点评 本题首先要选择研究对象,分析受力情况.其次确定电电动机刚好没有离开地面的临界条件,根据牛顿第二定律求解,难度适中.

练习册系列答案
相关题目
5.我国自行设计建造的世界第二斜拉索桥--上海南浦大桥,桥面高46m,主桥全长845m,引桥全长7500m,引桥建得这样长之后将( )
| A. | 增大汽车过桥的位移 | |
| B. | 增大汽车的重力垂直于引桥桥面向下的分力 | |
| C. | 增大汽车的重力平行于引桥桥面向下的分力 | |
| D. | 减小汽车的重力平行于引桥桥面向下的分力 |
10.静止的一价、二价铜离子经同一电场加速,再进入同一偏转电场后打在荧光屏上.不计离子的重力,以下说法中正确的是( )
| A. | 一价离子打到屏上的速度比二价离子速度大 | |
| B. | 离子经过加速电场时,一价离子所受电场力冲量小 | |
| C. | 从离开偏转电场时开始计时,则二价离子到达屏上所用的时间较长 | |
| D. | 两种离子打到屏上的位置到屏上中心点O的距离不相等 |
20. “影响平行板电容器的因素”的实验如图所示.平行板电容器的极板A与一灵敏的静电计相接,极板B接地.若极板B稍向上移动一点,由观察到的静电计指针变化作出的平行板电容器电容变小这一结论的依据是( )
“影响平行板电容器的因素”的实验如图所示.平行板电容器的极板A与一灵敏的静电计相接,极板B接地.若极板B稍向上移动一点,由观察到的静电计指针变化作出的平行板电容器电容变小这一结论的依据是( )
 “影响平行板电容器的因素”的实验如图所示.平行板电容器的极板A与一灵敏的静电计相接,极板B接地.若极板B稍向上移动一点,由观察到的静电计指针变化作出的平行板电容器电容变小这一结论的依据是( )
“影响平行板电容器的因素”的实验如图所示.平行板电容器的极板A与一灵敏的静电计相接,极板B接地.若极板B稍向上移动一点,由观察到的静电计指针变化作出的平行板电容器电容变小这一结论的依据是( )| A. | 两极板间电压不变,极板上的电量变大 | |
| B. | 两极板间电压不变,极板上的电量变小 | |
| C. | 极板上的电量几乎不变,两极板间的电压变大 | |
| D. | 极板上的电量几乎不变,两极板间的电压变小 |
7.如图所示,将原来不带电的绝缘导体AB,置于带正电的点电荷C所形成的电场中,则有( )
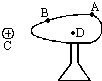

| A. | 绝缘导体上A、B两点的电势相等,且都高于大地的电势 | |
| B. | 绝缘导体上的感应电荷在导体内部一点D产生的场强大于点电荷C在D点产生场强的大小 | |
| C. | 有电场线终止在绝缘导体的表面上,且与导体表面垂直 | |
| D. | 用手接触A后,放开手和移除C,导体带正点 |
4. 如图所示,a、b、c三个α粒子,同时由同一点垂直于场强方向以不同的速率进入偏转电场,其轨迹如图,其中b恰好飞出电场,不计α粒子之间的相互作用力,由此可以肯定( )
如图所示,a、b、c三个α粒子,同时由同一点垂直于场强方向以不同的速率进入偏转电场,其轨迹如图,其中b恰好飞出电场,不计α粒子之间的相互作用力,由此可以肯定( )
 如图所示,a、b、c三个α粒子,同时由同一点垂直于场强方向以不同的速率进入偏转电场,其轨迹如图,其中b恰好飞出电场,不计α粒子之间的相互作用力,由此可以肯定( )
如图所示,a、b、c三个α粒子,同时由同一点垂直于场强方向以不同的速率进入偏转电场,其轨迹如图,其中b恰好飞出电场,不计α粒子之间的相互作用力,由此可以肯定( )| A. | 在b飞离电场的同时,a刚好打在负极板上 | |
| B. | b和c同时飞离电场 | |
| C. | 进入电场时,c的速度最小,a的速度最大 | |
| D. | 动能的增量相比,c的最小,a和b一样大 |
 三个形状相同但材料不同的物体A、B、C叠放存水平地面上,质量均为m=1kg,A与竖直墙壁通过水平轻绳相连,绳处于伸直状态.已知C和地面问的动摩擦因数μ1=0.2,B、C间的动摩擦因数μ2=0.3.现用一水平向右的力F拉着C匀速向右运动,发现A、B均不动.设最大静摩擦力等于滑动摩擦力,取g=10N/kg,求:
三个形状相同但材料不同的物体A、B、C叠放存水平地面上,质量均为m=1kg,A与竖直墙壁通过水平轻绳相连,绳处于伸直状态.已知C和地面问的动摩擦因数μ1=0.2,B、C间的动摩擦因数μ2=0.3.现用一水平向右的力F拉着C匀速向右运动,发现A、B均不动.设最大静摩擦力等于滑动摩擦力,取g=10N/kg,求: