题目内容
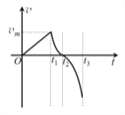
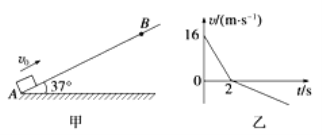
【题目】如图甲所示，有一足够长的粗糙斜面，倾角θ=37°，一滑块以初速度为v0=16m/s从底端A点滑上斜面，滑至B点后又返回到A点，滑块运动的v﹣t图象如图乙所示.（已知：sin37°=0.6，cos37°=0.8，重力加速度g=10m/s2）求：
（1）求物块与斜面之间的动摩擦因数；
（2）滑块再次回到A点时的速度大小；
（3）滑块在整个运动过程中所用的时间。
【答案】（1）0.25 （2）
（3）
【解析】（1）由图乙可知，滑块上滑时的加速度大小：a1=
m/s2=8m/s2，
由牛顿第二定律得，mgsin37°+μmgcos37°=ma1，
解得：μ=0.25．
（2）由图象可知，AB之间的距离： 
由B到A过程，受重力、支持力和摩擦力，根据牛顿第二定律有：
mgsinθ-μmgcosθ=ma2，
解得：a2=g（sin37°-μcos37°）=4m/s2，
由速度位移公式得，滑块再次回到A点时的速度： 
．
（3）由图象可知，滑块从A到B所用的时间t1=2s，
由速度时间公式得，滑块从B到A过程所用的时间： 
则滑块在整个运动过程中所用的时间：t=t1+t2=2（1+
）s．
练习册系列答案
三点一测快乐周计划系列答案
相关题目
