题目内容
2.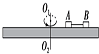 如图所示,两个可视为质点的、相同的木块a和B放在转盘上且木块a、B与转盘中心在同一条直线上,两木块用长为上的细绳连接,木块与转盘的最大静摩擦力均为各自重力的k倍,A放在距离转轴L处,整个装置能绕通过转盘中心的转轴O1O2转动.开始时,绳恰 好伸直但无弹力,现让该装置从静止转动,角速度缓慢增大,以下说法不正确的是( )
如图所示,两个可视为质点的、相同的木块a和B放在转盘上且木块a、B与转盘中心在同一条直线上,两木块用长为上的细绳连接,木块与转盘的最大静摩擦力均为各自重力的k倍,A放在距离转轴L处,整个装置能绕通过转盘中心的转轴O1O2转动.开始时,绳恰 好伸直但无弹力,现让该装置从静止转动,角速度缓慢增大,以下说法不正确的是( )| A. | 当ω>$\sqrt{\frac{2kg}{3L}}$时,A.B会相对于转盘滑动 | |
| B. | 当ω>$\sqrt{\frac{kg}{2L}}$时,绳子一定有弹力 | |
| C. | ω在$\sqrt{\frac{kg}{2L}}$<ω<$\sqrt{\frac{2kg}{3L}}$范围内增大时,B所受摩擦力变大 | |
| D. | ω在0<ω<$\sqrt{\frac{2kg}{3L}}$范围内增大时,A所受摩擦力一直变大 |
分析 开始角速度较小,绳子无拉力,两木块都靠静摩擦力提供向心力,B先到达最大静摩擦力,角速度继续增大,绳子会受到拉力,角速度继续增大,A的静摩擦力增大,当增大到最大静摩擦力时,开始发生相对滑动.
解答 解:A、当A所受的摩擦力达到最大静摩擦力时,A、B相对于转盘会滑动,对A有:kmg-T=mLω2,对B有:T+kmg=m•2Lω2,解得ω=$\sqrt{\frac{2kg}{3L}}$,当ω>$\sqrt{\frac{2kg}{3L}}$时,A、B相对于转盘会滑动.故A正确.
B、当B达到最大静摩擦力时,绳子开始出现弹力,kmg=m•2Lω2,
解得ω1=$\sqrt{\frac{kg}{2L}}$时,知ω>$\sqrt{\frac{kg}{2L}}$时,绳子一定有弹力.故B正确.
C、当角速度满足0<ω<$\sqrt{\frac{kg}{2L}}$时,B所受的摩擦力变大,ω在$\sqrt{\frac{kg}{2L}}$<ω<$\sqrt{\frac{2kg}{3L}}$范围内增大时,B所受摩擦力不变.故C错误.
D、当ω在0<ω<$\sqrt{\frac{2kg}{3L}}$范围内增大时,A所需要的向心力增大,则A所受摩擦力一直增大.故D正确.
本题选不正确的,故选:C
点评 解决本题的关键搞清木块向心力的来源,把握物体刚要滑动的条件,结合牛顿第二定律进行分析.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
13.客运轮船在九江至武汉之间做往返航班运行时刻表上(如下表所示),最右边一列是自九江起的公里数,根据表中数据,估算武汉至九江间长江的平均流速为多少?
| 上行 | 港名 | 下行 | 公里数 | ||
| 到港 | 离岗 | 离岗 | 到港 | ||
| 07:40 | 九江 | 22:00 | 0 | ||
| 10.30 | 武穴 | 20:00 | 19:30 | 50 | |
| 14:30 | 黄石 | 16:40 | 16:10 | 126 | |
| 不靠岸 | 鄂州 | 14:50 | 14:30 | 169 | |
| 21:30 | 武汉 | 11:00 | 269 | ||
10.如图所示,一木块受到垂直于倾斜墙面方向的推力F作用而处于静止状态,下列判断正确的是( )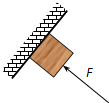

| A. | 墙面与木块间的弹力可能为零 | |
| B. | 墙面对木块的摩擦力方向沿倾斜墙面向上 | |
| C. | 在推力F逐渐增大过程中,木块将始终维持静止状态 | |
| D. | 在推力F逐渐增大过程中,木块所受墙面的摩擦力始终不变 |
17.关于磁场对通电直导线作用力的大小,下列说法中正确的是( )
| A. | 通电直导线跟磁场方向平行时作用力最大 | |
| B. | 通电直导线跟磁场方向垂直时作用力最大 | |
| C. | 通电直导线跟磁场方向有夹角时作用力最大 | |
| D. | 以上说法都不对 |
7. 如图,同一直线上有A、B、C三点,A、B处均固定着一正电荷,C处的负电荷受A、B的库仑力的合力记为F,若将C处的电荷向B移近一些,力F会( )
如图,同一直线上有A、B、C三点,A、B处均固定着一正电荷,C处的负电荷受A、B的库仑力的合力记为F,若将C处的电荷向B移近一些,力F会( )
 如图,同一直线上有A、B、C三点,A、B处均固定着一正电荷,C处的负电荷受A、B的库仑力的合力记为F,若将C处的电荷向B移近一些,力F会( )
如图,同一直线上有A、B、C三点,A、B处均固定着一正电荷,C处的负电荷受A、B的库仑力的合力记为F,若将C处的电荷向B移近一些,力F会( )| A. | 变小 | B. | 变大 | ||
| C. | 不变 | D. | 变大、变小均有可能 |
14.下列说法正确的是( )
| A. | 当研究一列火车全部通过桥所需的时间,因为火车上各点的运动状态相同,所以可以把火车视为质点 | |
| B. | 打点计时器是一种测量长度的仪器 | |
| C. | 位移和路程都是描述质点位置变动的物理量 | |
| D. | (n-1)末就是指第ns初 |
12.下面关于电源和电流的叙述正确的是( )
| A. | 电源的电动势大小与静电力做功W成正比,与移送电荷量q的大小成反比 | |
| B. | 电源的电动势越大,将其他形式的能转化为电能的本领越大 | |
| C. | 只要有大量的自由电荷便能产生电流 | |
| D. | 电流的方向就是自由电荷定向移动的方向 |
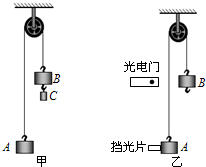 如图甲所示的装置叫做阿特伍德机,是英国数学家和物理学家阿特伍德(G•Atwood 1746-1807)创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.
如图甲所示的装置叫做阿特伍德机,是英国数学家和物理学家阿特伍德(G•Atwood 1746-1807)创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.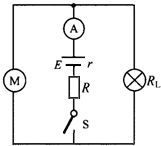 如图所示的电路中,电源电动势E=12V,内阻r=1Ω,电阻R的阻值为3Ω,指示灯RL的阻值为16Ω,电动机M线圈电阻RM为2Ω.当开关S闭合时,指示灯RL的电功率P=4W.求:
如图所示的电路中,电源电动势E=12V,内阻r=1Ω,电阻R的阻值为3Ω,指示灯RL的阻值为16Ω,电动机M线圈电阻RM为2Ω.当开关S闭合时,指示灯RL的电功率P=4W.求: