题目内容
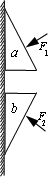a、b为完全相同的截面为直角的楔形物体，分别在垂直于斜边的恒力F1、F2作用下静止在相同的竖直墙面上，如图所示．下列说法正确的是（ ）分析：对A、B分别受力分析，然后分析一下除摩擦力以外的其它力，看看其它力是否有平衡的可能．
（1）若没有平衡的可能，则一定有摩擦力．
（2）若有平衡的可能，则可能有向上的摩擦力，也可能有向下的摩擦力，也可能没有摩擦力．
（1）若没有平衡的可能，则一定有摩擦力．
（2）若有平衡的可能，则可能有向上的摩擦力，也可能有向下的摩擦力，也可能没有摩擦力．
解答：解：对a受力分析如图1：
除摩擦力外的三个力不可能平衡，故一定有摩擦力．故a受四个力．
除摩擦力外对b受力分析如图2：
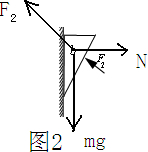
除摩擦力外，N，F2，mg三力有可能平衡．沿竖直方向和水平方向分解F2，设F2与竖直方向夹角为α则有：
F2cosα=mg…①
F2sinα=N…②
由①得F2=
…③
（1）若，F2=
没有摩擦力，此时b受3个力．
（2）若F2＞
，摩擦力向下，b受四个力．
（3）若F2＜
，摩擦力向上，b受四个力
A、当F2=
，b只受3个力．而a一定受四个力．故A错误
B、若F2远大于F1，则有可能b受到的向下的摩擦力大于a受到的摩擦力，故B错误．
C、当F2=
时，b受到的摩擦力为0，故C正确．
D、F1和F2有可能相等，但也有可能不等，故D错误．
故选：C
除摩擦力外的三个力不可能平衡，故一定有摩擦力．故a受四个力．
除摩擦力外对b受力分析如图2：
除摩擦力外，N，F2，mg三力有可能平衡．沿竖直方向和水平方向分解F2，设F2与竖直方向夹角为α则有：
F2cosα=mg…①
F2sinα=N…②
由①得F2=
| mg |
| cosα |
（1）若，F2=
| mg |
| cosα |
（2）若F2＞
| mg |
| cosα |
（3）若F2＜
| mg |
| cosα |
A、当F2=
| mg |
| cosα |
B、若F2远大于F1，则有可能b受到的向下的摩擦力大于a受到的摩擦力，故B错误．
C、当F2=
| mg |
| cosα |
D、F1和F2有可能相等，但也有可能不等，故D错误．
故选：C
点评：本题涉及受力分析、临界条件分析、平衡条件应用等知识．极易出错．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
