��Ŀ����
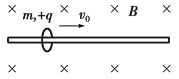
����Ŀ����ͼ��ʾ��AB��Ϊһ�뾶R=0��2m�Ĺ⻬![]() Բ�ι����EFΪһ���Ϊ30���Ĺ⻬б�棬б������һ����Ϊ0��1kg�ı�ľ��CD��ľ����¶�D��б��˵ľ���Ϊ15m����ʼʱľ�屻������һ����ҲΪ0��1kg������A���ɾ�ֹ��ʼ�»���ͨ��B���ˮƽ�׳�������һ��ʱ���ǡ����ƽ���ڱ�ľ��ķ�����ľ�壬����黬��ľ���ͬʱľ������������֪����뱡ľ���Ķ�Ħ������Ϊ��=
Բ�ι����EFΪһ���Ϊ30���Ĺ⻬б�棬б������һ����Ϊ0��1kg�ı�ľ��CD��ľ����¶�D��б��˵ľ���Ϊ15m����ʼʱľ�屻������һ����ҲΪ0��1kg������A���ɾ�ֹ��ʼ�»���ͨ��B���ˮƽ�׳�������һ��ʱ���ǡ����ƽ���ڱ�ľ��ķ�����ľ�壬����黬��ľ���ͬʱľ������������֪����뱡ľ���Ķ�Ħ������Ϊ��=![]() ��ȡg=10m/s2����
��ȡg=10m/s2����
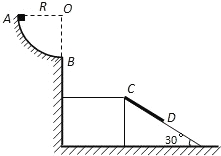
��1����鵽��B��ʱ��Բ�ι����ѹ����С��
��2�������ƽ���˶���ʱ�䣻
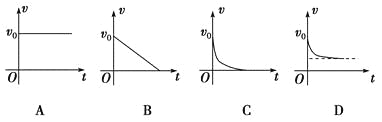
��3�����»�������ijʱ������ľ��ﵽ��ͬ�ٶȣ�������ٶ�Ϊ���
���𰸡���1��3N��2��![]() ��3��3��465m/s
��3��3��465m/s
�������������������1������A��B�Ĺ����л�е���غ㣬�ã�![]()
�ã�![]()
��鵽��B������G�����ϵĵ���F���ã���ţ�ٵڶ�����֪��![]()
�������ݵã�F=3N
��ţ�ٵ������ɿ�֪����鵽��B��ʱ��Բ�ι����ѹ����С��������ܵ���֧��������3N��������ֱ���£�
��2��������뿪B����ƽ���˶���ʱ��Ϊt1����ص㵽C��ʱ��ֱ����ķ��ٶ���vy����![]()
���ԣ�![]()
�֣�vy=gt1
���ԣ�![]()
��3����鵽��Cʱ�ĺ��ٶȣ�![]()
����C�������ܵ�������֧������Ħ���������ã���б�淽��
ma1=mgsin30�㩁��mgcos30��
�������ݵã�a1=2��5m/s2��������б�����£�
��ʱľ����б��ķ���Ma2=Mgsin30��+��mgcos30��
�������ݵã�a2=7��5m/s2��������б�����£�
�辭��ʱ��t2���ߵ��ٶ���ȣ���v+a1t2=a2t2
�������̣��������ݵã�![]()
���ߵĹ�ͬ�ٶȣ�v��=a2t2=7��5��0��462m/s=3��465m/s
�ù�����ľ���λ�ƣ�![]()
�����ߴﵽ��ͬ�ٶ�ʱ��ľ��û�л����ˣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�