题目内容
11. 在如图(甲)所示的电路中,R1、R2均为定值电阻,且R1=100Ω,R2阻值未知,R3是一滑动变阻器,当其滑片从左端滑至右端时,测得电源的路端电压随电流的变化图线如图(乙)所示,其中A、B两点是滑片在变阻器的左右两个不同端点得到的值.求:
在如图(甲)所示的电路中,R1、R2均为定值电阻,且R1=100Ω,R2阻值未知,R3是一滑动变阻器,当其滑片从左端滑至右端时,测得电源的路端电压随电流的变化图线如图(乙)所示,其中A、B两点是滑片在变阻器的左右两个不同端点得到的值.求:(1)定值电阻R2的阻值;
(2)电源的电动势E和内阻r;
(3)当滑动变阻器R3取何值时电源的输出功率最大?最大输出功率是多少?
分析 (1)电路电流与路端电压关系图象与纵轴的交点的纵坐标是电源的电动势,图象的斜率等于电源内阻,根据图象可以求出电源电动势与电源内阻.
(2)由图甲所示电路图可知,滑片在最右端时,只有电阻R2接入电路,此时对应与图乙所示图象的B点,由图象求出此时的路端电压与电路电流,然后由欧姆定律求出电阻阻值.
(3)当R3的滑片从最左端滑到最右端时,外电路总电阻从小于电源内阻r变至大于r,当外阻和内阻相等时,电源输出功率最大.
解答 解:(1)当P滑到R3的右端时,电路参数对应乙图中的B点,只有电阻R2接入电路,由图乙所示图象可知,U2=4V,I2=0.8A,
则定值电阻R2的阻值为:R2=$\frac{{U}_{2}}{{I}_{2}}$=$\frac{4}{0.8}$Ω=5Ω;
(2)将乙图中AB线延长,交U轴于20V处,所以电源的电动势为E=20V.图象斜率表示内阻为:r=$\frac{16-4}{0.8-0.2}$Ω=20Ω.
(3)当R3的滑片从最左端滑到最右端时,外电路总电阻从小于电源内阻r变至大于r,当外阻和内阻相等时,电源输出功率最大,则有:
r=R2+$\frac{{R}_{1}{R}_{3}}{{R}_{1}+{R}_{3}}$
代入:20=5$+\frac{100{R}_{3}}{100+{R}_{3}}$
解得:R3≈17.6Ω
其值为:P=$\frac{{E}^{2}}{4r}$=$\frac{2{0}^{2}}{4×20}$=5W.
答:(1)定值电阻R2的阻值为5Ω;
(2)电源的电动势为20V和内阻20Ω;
(3)当滑动变阻器R3取17.6Ω时电源的输出功率最大,电源的最大输出功率为5W.
点评 本题要理解电源的伏安特性曲线的意义,可由图线上两点的坐标建立方程组求解电源的电动势和内阻.

 在如图所示的装置中.表面粗糙的斜面固定在地面上.斜面的倾角为θ=30°;两个光滑的定滑轮的半径很小,用一根跨过定滑轮的细线连接甲、乙两物体,把甲物体放在斜面上且连线与斜面平行,把乙物体悬在空中,并使悬线拉直且偏离竖直方向α=60°.现同时释放甲、乙两物体,乙物体将在竖直平面内摆动,当乙物体运动经过最高点和最低点时,甲物体在斜面上均恰好末滑动.已知乙物体的质量为m=1kg,若重力加速度g取10m/s2.下列说法正确的是( )
在如图所示的装置中.表面粗糙的斜面固定在地面上.斜面的倾角为θ=30°;两个光滑的定滑轮的半径很小,用一根跨过定滑轮的细线连接甲、乙两物体,把甲物体放在斜面上且连线与斜面平行,把乙物体悬在空中,并使悬线拉直且偏离竖直方向α=60°.现同时释放甲、乙两物体,乙物体将在竖直平面内摆动,当乙物体运动经过最高点和最低点时,甲物体在斜面上均恰好末滑动.已知乙物体的质量为m=1kg,若重力加速度g取10m/s2.下列说法正确的是( )| A. | 乙物体运动经过最高点时悬线的拉力大小为5N | |
| B. | 乙物体运动经过最低点时悬线的拉力大小为20N | |
| C. | 斜面对甲物体的最大静摩擦力的大小为l5N | |
| D. | 甲物体的质量为2.5kg |
| A. | 同一实验过程中,O点位置可以移动 | |
| B. | 实验中,测力计必须保持与木板平行,读数时视线要正对测力计刻度 | |
| C. | 实验中,先将一个测力计沿某一方向拉到最大量程,然后只需调整另一测力计的大小和方向,把橡皮条另一端拉到O点 | |
| D. | 实验中,把橡皮条的另一端拉到O点时,两个测力计之间的夹角取90°,以便算出合力的大小 |
| A. | 2mgcosα | B. | 2mgsinα | C. | 2mg(1-sinα) | D. | 2mg(1+sinα) |
| A. | 灯泡的实际功率为50W | |
| B. | 灯泡的实际功率为25W | |
| C. | 通过灯泡的电流为额定电流的0.5倍 | |
| D. | 通过灯泡的电流为额定电流的0.25倍 |
| A. | 变大 | B. | 变小 | C. | 不变 | D. | 不能确定 |
| A. | 以甲车为参考系,乙车在向东行驶 | B. | 以甲车为参考系,乙车在向西行驶 | ||
| C. | 以乙车为参考系,地面在向东运动 | D. | 以乙车为参考系,甲车在向西行驶 |
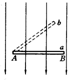
 如图所示,水平放置的光滑金属导轨M、N,平行地置于匀强磁场中,间距为d,磁场的磁感应强度为B,方向与导轨平面垂直,金属棒ab的质量为m,放在导轨上并且与导轨垂直,电源电动势为E,定值电阻阻值为R,其余部分电阻忽略不计,则当电键闭合瞬间,棒ab所受的安培力大小为多少?方向如何?棒的加速度为多少?
如图所示,水平放置的光滑金属导轨M、N,平行地置于匀强磁场中,间距为d,磁场的磁感应强度为B,方向与导轨平面垂直,金属棒ab的质量为m,放在导轨上并且与导轨垂直,电源电动势为E,定值电阻阻值为R,其余部分电阻忽略不计,则当电键闭合瞬间,棒ab所受的安培力大小为多少?方向如何?棒的加速度为多少? 一质量为M的圆环套在水平光滑杆上,用细线一端系一质量为m的小球挂在环上,当用力拉环做匀加速运动时,细线偏离竖直方向的夹角为θ,求拉力F的大小.
一质量为M的圆环套在水平光滑杆上,用细线一端系一质量为m的小球挂在环上,当用力拉环做匀加速运动时,细线偏离竖直方向的夹角为θ,求拉力F的大小.