题目内容
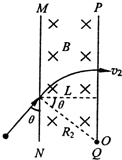
 如图所示,在真空区域内,有宽度为L的匀强磁场,磁感应强度为B,磁场方向垂直纸面向里,MN、PQ是磁场的边界.质量为m,带电量为-q的粒子,经电压U1加速后沿着与MN夹角为θ(0<θ<90°)的方向垂直磁感线射入匀强磁场B中,粒子刚好没能从PQ边界射出磁场,粒子加速前速度认为是零,不计重力的影响.
如图所示,在真空区域内,有宽度为L的匀强磁场,磁感应强度为B,磁场方向垂直纸面向里,MN、PQ是磁场的边界.质量为m,带电量为-q的粒子,经电压U1加速后沿着与MN夹角为θ(0<θ<90°)的方向垂直磁感线射入匀强磁场B中,粒子刚好没能从PQ边界射出磁场,粒子加速前速度认为是零,不计重力的影响.(1)求加速电压U1;
(2)为使粒子经电压U1加速射入磁场后沿直线运动,直至射出PQ边界,可在磁场区域加一匀强电场,求该电场的场强大小和方向;
(3)若粒子是经电压U2加速后射入磁场,粒子则刚好垂直PQ射出磁场,求加速电压U2;
(4)若PQ是一金属板,粒子垂直PQ射出磁场后被附近一带电量为+Q的固定带点小球俘获后,做半径为r的圆周运动,求粒子从PQ穿出时损失的动能.
分析:(1)根据几何关系求出做圆周运动的规定半径,由加速过程中电场力做的功等于粒子动能的变化量及圆周运动向心力公式即可求得加速电压;
(2)加匀强电场后,粒子在磁场中沿直线运动射出PQ边界的条件为电场力的方向与磁场力的方向相反,大小相等,根据Eq=qv1B即可的E;
(3)用(1)的方法求加速电压U2;
(4)由两电荷间的库仑力提供向心力求出速度,再分别求出动能,即可求出粒子从PQ穿出时损失的动能.
(2)加匀强电场后,粒子在磁场中沿直线运动射出PQ边界的条件为电场力的方向与磁场力的方向相反,大小相等,根据Eq=qv1B即可的E;
(3)用(1)的方法求加速电压U2;
(4)由两电荷间的库仑力提供向心力求出速度,再分别求出动能,即可求出粒子从PQ穿出时损失的动能.
解答:解:(1)由图可得R1(1+cosθ)=L
在磁场中做圆周运动:qv1B=m
在电场中加速:U1q=
m
得:U1=
(2)加匀强电场后,粒子在磁场中沿直线运动射出PQ边界的条件为电场力的方向与磁场力的方向相反,且Eq=qv1B
得:E=
E的方向垂直磁场方向斜向右下,与磁场边界夹角为:a=
-θ
(3)由图可得R2cosθ=L
同第(1)小题相同,得:U2=
(4)由两电荷间的库仑力提供向心力可得:k
=m
△Ek=
m
-
m
=
(
-k
)
答:(1)加速电压U1为
;
(2)该电场的场强大小为
,方向垂直磁场方向斜向右下,与磁场边界夹角为
-θ;
(3)若粒子是经电压U2加速后射入磁场,粒子则刚好垂直PQ射出磁场,加速电压U2为
;
(4)粒子从PQ穿出时损失的动能为
(
-k
).
在磁场中做圆周运动:qv1B=m
| ||
| R1 |
在电场中加速:U1q=
| 1 |
| 2 |
| v | 2 1 |
得:U1=
| qB2L2 |
| 2m(1+cosθ) |
(2)加匀强电场后,粒子在磁场中沿直线运动射出PQ边界的条件为电场力的方向与磁场力的方向相反,且Eq=qv1B
得:E=
| qB2L |
| m(1+cosθ) |
E的方向垂直磁场方向斜向右下,与磁场边界夹角为:a=
| π |
| 2 |
(3)由图可得R2cosθ=L
同第(1)小题相同,得:U2=
| qB2L2 |
| 2mcosθ |

(4)由两电荷间的库仑力提供向心力可得:k
| r2 |
| ||
| r |
△Ek=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 3 |
| 1 |
| 2 |
| q2B2L2 |
| mcos2θ |
| r |
答:(1)加速电压U1为
| qB2L2 |
| 2m(1+cosθ) |
(2)该电场的场强大小为
| qB2L |
| m(1+cosθ) |
| π |
| 2 |
(3)若粒子是经电压U2加速后射入磁场,粒子则刚好垂直PQ射出磁场,加速电压U2为
| qB2L2 |
| 2mcosθ |
(4)粒子从PQ穿出时损失的动能为
| 1 |
| 2 |
| q2B2L2 |
| mcos2θ |
| r |
点评:该题主要考查了带电粒子在加速电场和磁场中的运动.要求同学们能正确画出粒子运动的轨迹,并根据几何关系求得轨道半径,能用向心力公式和周期公式解题,难度较大,属于难题.

练习册系列答案
相关题目
 (2013?泰安三模)如图所示,在真空区域Ⅰ、Ⅱ中存在两个匀强电场.其电场线方向竖直向下,在区域Ⅰ中有一个带负电的油滴沿电场线以速度v0匀速下落,并进入区域Ⅱ(电场范围足够大).能描述粒子在两个电场中运动的速度--时间图象是(以v0方向为正方向)( )
(2013?泰安三模)如图所示,在真空区域Ⅰ、Ⅱ中存在两个匀强电场.其电场线方向竖直向下,在区域Ⅰ中有一个带负电的油滴沿电场线以速度v0匀速下落,并进入区域Ⅱ(电场范围足够大).能描述粒子在两个电场中运动的速度--时间图象是(以v0方向为正方向)( ) (2008?和平区模拟)如图所示,在真空区域内,有宽度为L的匀强磁场,磁感应强度为B,磁场方向垂赢纸面向里,MN、PQ是磁场的边界.质量为m,带电量为-q的粒子,先后两次沿着与MN夹角为θ(0<θ<90°)的方向垂直磁感线射入匀强磁场B中,第一次,:粒子是经电压U1加速后射入磁场,粒子刚好没能从PQ边界射出磁场.第二次粒子是经电压U2加速后射入磁场,粒子则刚好垂直PQ射出磁场.不计重力的影响,粒子加速前速度认为是零,求:
(2008?和平区模拟)如图所示,在真空区域内,有宽度为L的匀强磁场,磁感应强度为B,磁场方向垂赢纸面向里,MN、PQ是磁场的边界.质量为m,带电量为-q的粒子,先后两次沿着与MN夹角为θ(0<θ<90°)的方向垂直磁感线射入匀强磁场B中,第一次,:粒子是经电压U1加速后射入磁场,粒子刚好没能从PQ边界射出磁场.第二次粒子是经电压U2加速后射入磁场,粒子则刚好垂直PQ射出磁场.不计重力的影响,粒子加速前速度认为是零,求: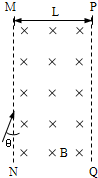 如图所示,在真空区域内,有宽度为L的匀强磁场,磁感应强度为B,磁场方向垂直纸面向里,MN、PQ是磁场的边界.质量为m,带电量为-q的粒子,先后两次沿着与MN夹角为θ(0<θ<90°)的方向垂直磁感线射入匀强磁场B中,第一次,粒子是经电压U1加速后射入磁场,粒子刚好没能从PQ边界射出磁场.第二次粒子是经电压U2加速后射入磁场,粒子则刚好垂直PQ射出磁场.不计重力的影响,粒子加速前速度认为是零,求:加速电压
如图所示,在真空区域内,有宽度为L的匀强磁场,磁感应强度为B,磁场方向垂直纸面向里,MN、PQ是磁场的边界.质量为m,带电量为-q的粒子,先后两次沿着与MN夹角为θ(0<θ<90°)的方向垂直磁感线射入匀强磁场B中,第一次,粒子是经电压U1加速后射入磁场,粒子刚好没能从PQ边界射出磁场.第二次粒子是经电压U2加速后射入磁场,粒子则刚好垂直PQ射出磁场.不计重力的影响,粒子加速前速度认为是零,求:加速电压