Question

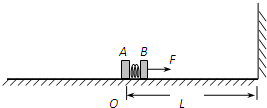（2011?湖北模拟）如图所示，水平面O点的右侧光滑，左侧粗糙．O点到右侧竖直墙壁的距离为L，一系统由可看作质点的A、B两木块和一短而硬（即劲度系数很大）的轻质弹簧构成．A，B两木块的质量均为m，弹簧夹在A与B之间，与二者接触而不固连．让A、B压紧弹簧，并将它们锁定，此时弹簧的弹性势能为E₀该系统在O点从静止开始在水平恒力F作用下幵始向右运动，当运动到离墙S=L/4时撤去恒力F，撞击墙壁后以原速率反弹，反弹后当木块A运动到O点前解除锁定．通过遥控解除锁定时，弹簧可瞬时恢复原长．求
（1）解除锁定前瞬间，A，B的速度多少？
（2）解除锁定后瞬间，A，B的速度分别为多少？
（3）解除锁定后F、L、E₀、m、满足什么条件时，B具有的动能最小．在这种情况下A能运动到距O点最远的距离为多少？（己知A与粗糙水平面间的动摩擦因数为u）

Answer 1

分析：（1）由于撞击墙壁后以原速率反弹，则得解除锁定前瞬间A、B的速度大小等于撤去恒力F时的速度大小，根据动能定理求解．
（2）解除锁定的过程，A、B和弹簧组成的系统动量守恒、机械能守恒，可由两大守恒求出解除锁定后瞬间A，B的速度．
（3）全部的机械能全部转化给A，B具有的动能最小，由（2）结果求出A的速度，再由动能定理求解A能运动到距O点最远的距离．

解答：解：（1）由于撞击墙壁后以原速率反弹，所以解除锁定前瞬间A、B的速度大小相等且等于撤去恒力F时的速度大小，根据动能定理有：
   f(

3

4

L)=

1

2

(2m)v2
解得：v=

3FL 4m

（2）设解除锁定后，A、B速度分别为v₁、v₂；（m₁=m₂=m）
由于弹开瞬时，系统动量守恒：2mv=m₁v₁+m₂v₂
由于解除锁定过程中系统机械能守恒，则有：

1

2

(2m)v2+E₀=

1

2

m1

v

2 1

+

1

2

m2

v

2 2

由上面三式联立解得：v₁=

3FL 4m

+

E0 m

，v₂=

3FL 4m

-

E0 m

，或v₁=

3FL 4m

-

E0 m

，v₂=

3FL 4m

+

E0 m

．
由于v₁＞v₂，所以应该取：v₁=

3FL 4m

+

E0 m

，v₂=

3FL 4m

-

E0 m

．
（3）若解除锁定后B物体的最小动能应为零，即全部的机械能全部转化给A，即：v₂=

3FL 4m

-

E0 m

=0，
解得：E₀=

3

4

FL
将上式代入v₁可得最大值：v_1m=

3FL m

根据动能定理得：-μmgSm=0-

1

2

m

v

2 1m

所以A距O点的最远距离为：S_m=

3FL

2μmg

答：
（1）解除锁定前瞬间，A，B的速度是

3FL 4m

．
（2）解除锁定后瞬间，A，B的速度分别为

3FL 4m

+

E0 m

和

3FL 4m

-

E0 m

．
（3）A能运动到距O点最远的距离为

3FL

2μmg

．

点评：本题过程较多，但所蕴含的物理规律并不太难，按程序法进行分析，加以讨论分析，可以正确解答．