��Ŀ����
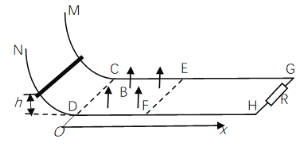
����Ŀ����ͼ��ʾ��CEG��DFH�������㹻���ġ�ˮƽ���õ�ƽ�н������죬������ΪL����CDFE������ڴ�ֱ�ڵ���ƽ�����ϵ��н���ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB��������Ҷ˽���һ��ֵΪR�ĵ��裬�����⻬�������MC��NDƽ�����ӡ��ֽ�һ��ֵΪR������Ϊm�ĵ���������������h�ߴ��ɾ�ֹ�ͷţ����������ǡͣ�ڴų����ұ߽�EF��������������費�ƣ�EF��ർ��⻬���Ҳർ��ֲڣ��뵼����䶯Ħ������Ϊ��������ԭ��λ�ڴų���߽�CD�������ص������ҵ�������x����֪��������н�ų����˶����ٶ���λ�ƾ��ȱ仯���������ϵʽ��![]() ��v0Ϊ����������н�ų��ij��ٶȡ���
��v0Ϊ����������н�ų��ij��ٶȡ���
(1)�н�ų�����Ŀ���d��
(2)������˶���![]() ���ٶ�a��
���ٶ�a��
(3)������������������4h�ߴ��ɾ�ֹ�ͷţ���������յ�λ������x����һ�����е�����ϲ����Ľ�����Q��
���𰸡�(1)![]() ��(2)
��(2)![]() ��������x�Ḻ����(3)
��������x�Ḻ����(3) ![]() ��
��![]()
��������
(1)�����������������»�����е���غ㣬��
![]()
![]()
�������CD��EF����
![]()
![]()
(2)������˶���
![]() ��
��
�ٶ�Ϊ![]() ����
����
![]()
������ʽ����
![]()
��
![]()
![]()
������ļ��ٶ�
![]()
������x�Ḻ����
(3)�����������������»�����
![]()
![]()
������˶���EF�����ٶ�Ϊ![]() ����
����
![]()
���ڴֲڹ���ϼ��ٻ��У����ٶ�Ϊ
![]()
![]()
![]()
��������н�ų����˶����ٶȴ�![]() ��С��
��С��![]() ���˷�����������Ϊ
���˷�����������Ϊ
![]()
�˹����е���R�ϲ����Ľ�����Ϊ
![]()

 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�