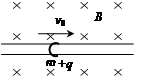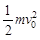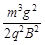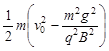题目内容
(2011·厦门模拟)(18分)如图所示,质量为m,电荷量为e的电子从坐标原点O处沿xOy平面射入第一象限内,射入时的速度方向不同,但大小均为v0.现在某一区域内加一方向向外且垂直于xOy平面的匀强磁场,磁感应强度大小为B,若这些电子穿过磁场后都能垂直地射到与y轴平行的荧光屏MN上,求:

(1)电子从y轴穿过的范围;
(2)荧光屏上光斑的长度;
(3)所加磁场范围的最小面积.

(1)电子从y轴穿过的范围;
(2)荧光屏上光斑的长度;
(3)所加磁场范围的最小面积.
(1) 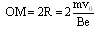 (2)
(2)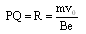 (3)
(3) 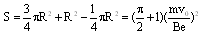
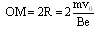 (2)
(2)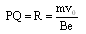 (3)
(3) 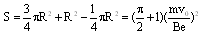
(1)设粒子在磁场中运动的半径为R,由牛顿第二定律得: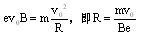 (2分)
(2分)
电子从y轴穿过的范围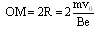 (2分)
(2分)
(2)如图所示,初速度沿x轴正方向的电子沿弧OA运动到荧光屏MN上的P点, (1分)
初速度沿y轴正方向的电子沿弧OC运动到荧光屏MN上的Q点(1分)
由几何知识可得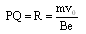 (2分)
(2分)
(3)取与x轴正方向成θ角的方向射入的电子为研究对象,其射出磁场的点为E(x,y),因其射出后能垂直打到荧光屏MN上,故有:
x=-Rsinθ (2分)
y=R+Rcosθ (2分)
即x2+(y-R)2=R2 (2分)
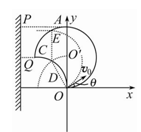
又因为电子沿x轴正方向射入时,射出的边界点为A点;沿y轴正方向射入时,射出的边界点为C点,故所加最小面积的磁场的边界是以(0,R)为圆心、R为半径的圆的一部分,如图中实线圆弧所围区域,所以磁场范围的最小面积为: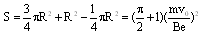 (4分)
(4分)
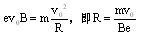 (2分)
(2分)电子从y轴穿过的范围
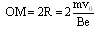 (2分)
(2分)(2)如图所示,初速度沿x轴正方向的电子沿弧OA运动到荧光屏MN上的P点, (1分)
初速度沿y轴正方向的电子沿弧OC运动到荧光屏MN上的Q点(1分)
由几何知识可得
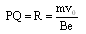 (2分)
(2分)(3)取与x轴正方向成θ角的方向射入的电子为研究对象,其射出磁场的点为E(x,y),因其射出后能垂直打到荧光屏MN上,故有:
x=-Rsinθ (2分)
y=R+Rcosθ (2分)
即x2+(y-R)2=R2 (2分)

又因为电子沿x轴正方向射入时,射出的边界点为A点;沿y轴正方向射入时,射出的边界点为C点,故所加最小面积的磁场的边界是以(0,R)为圆心、R为半径的圆的一部分,如图中实线圆弧所围区域,所以磁场范围的最小面积为:
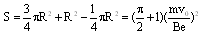 (4分)
(4分) 
练习册系列答案
相关题目


 向上移动
向上移动