题目内容
 (2011?赤峰一模)如图所示,平行导轨MN和PQ相距0.5m,电阻可忽略.其水平部分是粗糙的,置于0.60T竖直向上的匀强磁场中,倾斜部分是光滑的,该处没有磁场.导线a和b质量均为0.20kg,电阻均为0.15Ω,a、b相距足够远,b放在水平导轨上.a从斜轨上高0.050m处无初速释放.求:
(2011?赤峰一模)如图所示,平行导轨MN和PQ相距0.5m,电阻可忽略.其水平部分是粗糙的,置于0.60T竖直向上的匀强磁场中,倾斜部分是光滑的,该处没有磁场.导线a和b质量均为0.20kg,电阻均为0.15Ω,a、b相距足够远,b放在水平导轨上.a从斜轨上高0.050m处无初速释放.求:(1)回路的最大感应电流是多少?
(2)如果导线与导轨间的动摩擦因数μ=0.10,当导线b的速率达到最大值时,导线a的加速度是多少?
分析:(1)a导线无初速释放,在进入磁场前机械能守恒,进入磁场后,受向右的安培力和向右的摩擦力,做减速运动,所以进入磁场时的速度最大,产生的感应电动势最大,感应电流最大.
(2)a导线进入磁场后,做减速运动,b导线受到向左的安培力和向右的摩擦力,先向左加速,整个电路的电动势减小,电流减小,安培力减小,所以b导线的加速度减小,当b导线的加速度减小到0时,速率最大.求出此时的电流,从而可求出a导线的安培力以及摩擦力,根据牛顿第二定律,求出导线a的加速度.
(2)a导线进入磁场后,做减速运动,b导线受到向左的安培力和向右的摩擦力,先向左加速,整个电路的电动势减小,电流减小,安培力减小,所以b导线的加速度减小,当b导线的加速度减小到0时,速率最大.求出此时的电流,从而可求出a导线的安培力以及摩擦力,根据牛顿第二定律,求出导线a的加速度.
解答:解:(1)a棒在没有磁场的倾斜轨道上下滑时,机械能守恒,进入水平轨道时a棒的速度vm,
mgh=
mvm2
vm=
=
=1m/s,
此时a棒速度最大,进入磁场切割磁感线,产生的感应电流最大
L=
=
=
=1A.
(2)当a、b棒组成的闭合回路中有感应电流时,a、b棒都受安培力作用,a棒受安培力向右、摩擦力向右,b棒受安培力向左,摩擦力向右.
f=μmg=0.10×0.20×10=0.2N
F=BImL=0.60×1×0.5=0.3N
因为F>f所以b棒开始向左加速.a棒是向左做减速运动,b棒的速度增大时,电路中的感应电流减小,b棒受的安培力在减小,当电流减为I'时,加速度为0,这时满足:
μmg=BI′L
此时a棒受到的摩擦力和安培力方向都向右,a棒的加速度.
μmg+BI′L=ma
代入数据 a=2m/s2.
mgh=
| 1 |
| 2 |
vm=
| 2gh |
| 2×10×0.050 |
此时a棒速度最大,进入磁场切割磁感线,产生的感应电流最大
L=
| E |
| R |
| BLvm |
| 2r |
| 0.60×0.5×1 |
| 2×0.15 |
(2)当a、b棒组成的闭合回路中有感应电流时,a、b棒都受安培力作用,a棒受安培力向右、摩擦力向右,b棒受安培力向左,摩擦力向右.
f=μmg=0.10×0.20×10=0.2N
F=BImL=0.60×1×0.5=0.3N
因为F>f所以b棒开始向左加速.a棒是向左做减速运动,b棒的速度增大时,电路中的感应电流减小,b棒受的安培力在减小,当电流减为I'时,加速度为0,这时满足:
μmg=BI′L
此时a棒受到的摩擦力和安培力方向都向右,a棒的加速度.
μmg+BI′L=ma
代入数据 a=2m/s2.
点评:解决本题的关键能够正确受力分析,结合牛顿定律,判断导线的运动状况.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
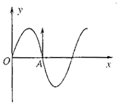 (2011?赤峰一模)一列横波沿直线传播,某时刻的波形如图所示,质点A的平衡位置与坐标原点O相距0.5m,此时质点A沿正方向运动,再经0.02s第一次到达最大位移.由此可知:( )
(2011?赤峰一模)一列横波沿直线传播,某时刻的波形如图所示,质点A的平衡位置与坐标原点O相距0.5m,此时质点A沿正方向运动,再经0.02s第一次到达最大位移.由此可知:( )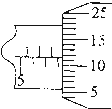 (2011?赤峰一模)(1)用螺旋测微器(千分尺)测小球直径时,示数如图所示,则小球的直径为
(2011?赤峰一模)(1)用螺旋测微器(千分尺)测小球直径时,示数如图所示,则小球的直径为 .
.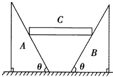 (2011?赤峰一模)如图所示,两个截面为三角形的实心铁块A、B并排放在粗糙水平地面上,一截面为矩形的实心铁块C水平地架在两铁块的光滑斜面上,系统处于静止状态.已知三个铁块的重力分别为GA=GB=100N、GC=10N,θ=60°,求
(2011?赤峰一模)如图所示,两个截面为三角形的实心铁块A、B并排放在粗糙水平地面上,一截面为矩形的实心铁块C水平地架在两铁块的光滑斜面上,系统处于静止状态.已知三个铁块的重力分别为GA=GB=100N、GC=10N,θ=60°,求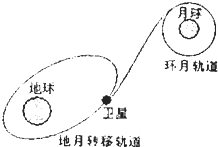 (2011?赤峰一模)2010年10月1日18时59分57秒,中国自主研制的第二颗绕月探测卫星“嫦娥二号”成功发射.此次发射由火箭直接将卫星送到近地点200公里,远地点38万公里的地月转移轨道后,再飞向月球,被月球捌获后,最终进入100公里的环月轨道,对月球进行探测.设月球半径为R(km),月球质量为M(kg),这个过程可简化为如图模型,根据题中信息和所学知识判断下列说法错误的是( )
(2011?赤峰一模)2010年10月1日18时59分57秒,中国自主研制的第二颗绕月探测卫星“嫦娥二号”成功发射.此次发射由火箭直接将卫星送到近地点200公里,远地点38万公里的地月转移轨道后,再飞向月球,被月球捌获后,最终进入100公里的环月轨道,对月球进行探测.设月球半径为R(km),月球质量为M(kg),这个过程可简化为如图模型,根据题中信息和所学知识判断下列说法错误的是( )