题目内容
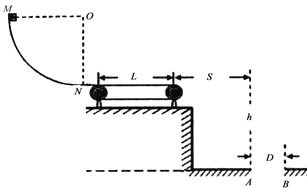
【题目】如图所示，一段光滑的圆轨道MN竖直固定放置，末端N与一长L=0．8m的水平传送带相切，水平衔接部分摩擦不计，传动轮（轮半径很小）作顺时针转动，带动传送带以恒定的速度ν0运动。传送带离地面的高度h=1．25m，其右侧地面上有一直径D=0．5m的圆形洞，洞口最左端的A点离传送带右端的水平距离S =1m， B点在洞口的最右端。现使质量为m=0．5kg的小物块从M点由静止开始释放，到达N点时的速度为2m/s.经过传送带后做平抛运动，最终落入洞中，传送带与小物块之间的动摩擦因数μ=0．5。 g取10m/s2。求：
（1）小物块到达圆轨道末端N时对轨道的压力；
（2）若ν0=3m/s,求物块在传送带上运动的时间；
（3）若要使小物块能落入洞中，求ν0应满足的条件。
【答案】（1）15N；（2）0.3s；（3）2m/s<v<3m/s
【解析】（1）设物块滑到圆轨道末端速度ν1，根据机械能守恒定律得：mgR=
mv12设物块在轨道末端所受支持力的大小为F，根据牛顿第二定律得： 
联立以上两式代入数据得：F=15N根据牛顿第三定律，对轨道压力大小为15N，方向竖直向下（2）物块在传送带上加速运动时，由μmg=ma，得a=μg=5m/s2加速到与传送带达到同速所需要的时间
位移
匀速时间
故T=t1+t2=0.3s（3）物块由传送带右端平抛h=
gt2恰好落到A点s=v2t得ν2=2m/s恰好落到B点D+s=ν3t得ν3=3m/s当物块在传送带上一直加速运动时，做平抛运动的速度最大，假设物块在传送带上达到的最大速度为v，由动能定理：umgL=
mv2-
mv12得：v2=12，且12＞9，所以物块在传送带上达到的最大速度大于能进入洞口的最大速度，所以ν0应满足的条件是3m/s＞ν0＞2m/s.
