题目内容
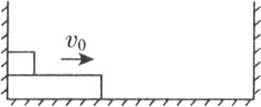
如图所示,在光滑四分之一圆弧轨道的顶端a点,质量为m的物块(可视为质点)由静止开始下滑,经圆弧最低点b滑上粗糙水平面,圆弧轨道在b点与水平轨道平滑相接,物块最终滑至c点停止.若圆弧轨道半径为R,物块与水平面间的动摩擦因数为μ,下列说法正确的是( )
A.物块滑到b点时的速度为
B.物块滑到b点时对b点的压力是3mg
C.c点与b点的距离为
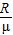
D.整个过程中物块机械能损失了mgR
【答案】分析:由机械能守恒可求得物块滑到b点时的速度,由向心力公式可求得b点对物体的支持力,由牛顿第三定律可知物块对b点的压力;
由动能定理可求得bc两点的距离;由摩擦力做功可求得机械能的损失.
解答:解:A、由机械能守恒可知,mgR=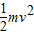 ,解得b点时的速度为
,解得b点时的速度为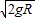 ,故A错误;
,故A错误;
B、b点时,物体受重力、支持力而做圆周运动,则由F-mg=m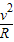 可得,支持力F=3mg,由牛顿第三定律可知,物块对b点的压力为3mg; 故B正确;
可得,支持力F=3mg,由牛顿第三定律可知,物块对b点的压力为3mg; 故B正确;
C、对全程由动能定理可知,mgR-μmgs=0,解得bc两点间的距离为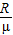 ,故C正确;
,故C正确;
D、在滑动过程中,摩擦力所做的功等于机械能的损失,故机械能损失了μmgs=mgR,故D正确;
故选BCD.
点评:在功能关系中,要注意明确:重力做功等于重力势能的改变量;而摩擦力做功等于机械能的改变量.
由动能定理可求得bc两点的距离;由摩擦力做功可求得机械能的损失.
解答:解:A、由机械能守恒可知,mgR=
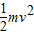 ,解得b点时的速度为
,解得b点时的速度为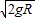 ,故A错误;
,故A错误;B、b点时,物体受重力、支持力而做圆周运动,则由F-mg=m
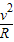 可得,支持力F=3mg,由牛顿第三定律可知,物块对b点的压力为3mg; 故B正确;
可得,支持力F=3mg,由牛顿第三定律可知,物块对b点的压力为3mg; 故B正确;C、对全程由动能定理可知,mgR-μmgs=0,解得bc两点间的距离为
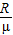 ,故C正确;
,故C正确;D、在滑动过程中,摩擦力所做的功等于机械能的损失,故机械能损失了μmgs=mgR,故D正确;
故选BCD.
点评:在功能关系中,要注意明确:重力做功等于重力势能的改变量;而摩擦力做功等于机械能的改变量.

练习册系列答案
相关题目