题目内容
【题目】如图所示,AO、AB、AC是竖直平面内的三根固定的细杆,A、O位于同一圆周上,A点位于圆周的最高点,O点位于圆周的最低点,每一根细杆上都套有一个光滑的小球(图中未画出),三个环都从A点无初速地释放,用T1、T2、T3表示各环到O、B、C时所用的时间,则( )
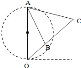
A. T1>T2>T3 B. T3<T1<T2 C. T1<T2<T3 D. T3>T1>T2
【答案】D
【解析】
小环沿杆下滑做匀加速直线运动,设∠OAB为θ,∠OAC为α,由匀变速运动规律求出小球运动的加速度和位移,根据匀加速直线运动位移时间公式表示出时间即可求解。
如图:

小环沿杆下滑做匀加速直线运动,设∠OAB为θ,∠OAC为α,圆的半径为r,
则 小环沿AO下滑时,做自由落体运动,时间为:
![]()
由匀变速运动规律得,滑环滑到B1点的时间:![]()
而由图可知,滑到B点的时间T2<T2′=T1
同样根据匀变速运动规律可得滑到C1的时间:![]()
而由图可知,滑到C点的时间T3>T3′=T1
故有,T3>T1>T2,
故应选:D。

练习册系列答案
相关题目