题目内容
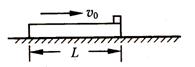
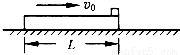
 质量M=9kg、长L=1m的木板在动摩擦因数μ1=0.1的水平地面上向右滑行,当速度v0=2m/s时,在木板的右端轻放一质量m=1kg的小物块如图所示.当小物块刚好滑到木板左端时,物块和木板达到共同速度.取g=10m/s2,求:
质量M=9kg、长L=1m的木板在动摩擦因数μ1=0.1的水平地面上向右滑行,当速度v0=2m/s时,在木板的右端轻放一质量m=1kg的小物块如图所示.当小物块刚好滑到木板左端时,物块和木板达到共同速度.取g=10m/s2,求:
(1)从木块放到木板上到它们达到相同速度所用的时间t;
(2)小物块与木板间的动摩擦因数μ2.
解:(1)设木板在时间t内的位移为x1;木块的加速度大小为a1,木板的加速度大小为a2,时间t内的位移为x2
则有x1=v0t-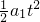 ①
①
x2=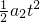 ②
②
x1=L+x2③
又v0-a1t=a2t④
其中a1=μg,a2=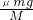 ;
;
代入数据得t=1s ⑤
(2)根据牛顿第二定律,有μ1(M+m)g+μ2mg=Ma1⑥
μ2mg=ma2⑦
解得μ2=0.08⑧
答:(1)从木块放到木板上到它们达到相同速度所用的时间t为1秒;
(2)小物块与木板间的动摩擦因数为0.08.
分析:(1)对木块好滑块分别运用速度时间公式、位移时间公式列式,然后联立求解;
(2)对木块和长木板分别受力分析,然后运动牛顿第二定律列式求解.
点评:本题关键是先根据运动学公式列式后联立求解出时间,然后再受力分析后根据牛顿第二定律列式求解;对于第一问,可以以长木板为参考系列式求解,会使得问题大大简化.
则有x1=v0t-
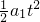 ①
①x2=
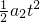 ②
②x1=L+x2③
又v0-a1t=a2t④
其中a1=μg,a2=
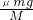 ;
;代入数据得t=1s ⑤
(2)根据牛顿第二定律,有μ1(M+m)g+μ2mg=Ma1⑥
μ2mg=ma2⑦
解得μ2=0.08⑧
答:(1)从木块放到木板上到它们达到相同速度所用的时间t为1秒;
(2)小物块与木板间的动摩擦因数为0.08.
分析:(1)对木块好滑块分别运用速度时间公式、位移时间公式列式,然后联立求解;
(2)对木块和长木板分别受力分析,然后运动牛顿第二定律列式求解.
点评:本题关键是先根据运动学公式列式后联立求解出时间,然后再受力分析后根据牛顿第二定律列式求解;对于第一问,可以以长木板为参考系列式求解,会使得问题大大简化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013?潍坊一模)质量M=9kg、长L=1m的木板在动摩擦因数μ1=0.1的水平地面上向右滑行,当速度v0=2m/s时,在木板的右端轻放一质量m=1kg的小物块如图所示.当小物块刚好滑到木板左端时,物块和木板达到共同速度.取g=10m/s2,求:
(2013?潍坊一模)质量M=9kg、长L=1m的木板在动摩擦因数μ1=0.1的水平地面上向右滑行,当速度v0=2m/s时,在木板的右端轻放一质量m=1kg的小物块如图所示.当小物块刚好滑到木板左端时,物块和木板达到共同速度.取g=10m/s2,求: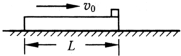 质量M=9kg、长L=1m的木板在动摩擦因数μ=0.1的水平地面上向右滑行,当速度υ0=2m/s时,在木板的右端轻放一质量m=1kg的小物块如图所示.当小物块刚好滑到木板左端时,物块和木板达到共同速度.取g=10m/s2,求:
质量M=9kg、长L=1m的木板在动摩擦因数μ=0.1的水平地面上向右滑行,当速度υ0=2m/s时,在木板的右端轻放一质量m=1kg的小物块如图所示.当小物块刚好滑到木板左端时,物块和木板达到共同速度.取g=10m/s2,求: