题目内容
如图所示A、B两物体叠放在光滑的斜面上，其质量分别为M、m，斜面倾角为θ，A、B一起运动，A对B的支持力为FN，A对B的摩擦力为Ff，下列说法正确的是（ ）分析：先对整体进行受力分析，由牛顿第二定律可求得整体运动的加速度；再对B单独分析，由运动的合成与分解可求得水平及竖直方向上的运动情况，再分别对这两个方向利用牛顿第二定律可求得支持力及摩擦力．
解答：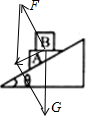
解：对整体分析可知，整体受重力、支持力而向下做匀加速直线运动；由牛顿第二定律可知，（M+m）gsinθ=（M+m）a；解得：a=gsinθ；
对B分析可知，B在水平方向具有ax=acosθ=gsinθcosθ；ay=asinθsinθ；
水平方向，B受A的摩擦力，则由牛顿第二定律可知，f=max=mgcosθsinθ=
，
竖直方向，B受到重力和支持力，则由牛顿第二定律可知，mg-FN=may；
FN=mg-mgsin2θ=mgcos2θ
故选C．
解：对整体分析可知，整体受重力、支持力而向下做匀加速直线运动；由牛顿第二定律可知，（M+m）gsinθ=（M+m）a；解得：a=gsinθ；对B分析可知，B在水平方向具有ax=acosθ=gsinθcosθ；ay=asinθsinθ；
水平方向，B受A的摩擦力，则由牛顿第二定律可知，f=max=mgcosθsinθ=
| mgsin2θ |
| 2 |
竖直方向，B受到重力和支持力，则由牛顿第二定律可知，mg-FN=may；
FN=mg-mgsin2θ=mgcos2θ
故选C．
点评：本题注意将加速度分解后，利用速度的合成与分解的方法分解加速度，可以直接求出水平方向的摩擦力及支持力，难度有了大幅的降低．
练习册系列答案
相关题目
（2011?静安区一模）如图所示A、B两物体用跨过定滑轮的轻绳相连，A的质量大于B的质量，A放置在水平地板上，与地板的动摩擦因数恒定，对A施加水平向右的外力F，使A沿地板向右运动，B保持匀减速上升．设A受绳的拉力为T，受地面的弹力为N，受摩擦力为f．以下判断正确的是（ ）
如图所示A．B两物体先后从同一地点以相同的初速度作匀变速直线运动的速度图象，下列说法正确的是（ ）
（2011?徐汇区模拟）如图所示A、B两物体用跨过定滑轮的轻绳相连，A的质量大于B的质量，A放置在水平地板上，与地板的动摩擦因数恒定，对A施加水平向右的外力F，使A沿地板向右运动，B保持匀速上升．设A受绳的拉力为T，受地面的弹力为N，受摩擦力为f．以下判断正确的是（ ）
如图所示A、B两物体做直线运动的图象，则（ ）