题目内容
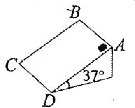 如图所示,楔形斜面体倾角为37°,其BC长为0.8m,AB宽为0.6m,一重为25N的木块原先在斜面体上部,它与斜面间的动摩擦因数为0.6,要使木块沿对角线AC方向匀速下滑,(sin37°=0.6,cos37°=0.8),需要对它施加方向平行于斜面的力F,则F的大小和方向为( )
如图所示,楔形斜面体倾角为37°,其BC长为0.8m,AB宽为0.6m,一重为25N的木块原先在斜面体上部,它与斜面间的动摩擦因数为0.6,要使木块沿对角线AC方向匀速下滑,(sin37°=0.6,cos37°=0.8),需要对它施加方向平行于斜面的力F,则F的大小和方向为( )分析:以木块为研究对象,分析受力情况,将重力分解为沿斜面方向和垂直于斜面方向两个分力.将力分为斜面平面和垂直于斜面平面两个平面进行研究,根据平衡条件和数学知识求解平行于斜面的力的大小和方向.
解答:解:N=mgcos37°=25×0.8=20N.f=μN=0.6×20=12(N)
重力沿斜面向下的分量:mgsinθ=15(N)
在斜面这一平面内,f、F与重力沿斜面向下的分量mgsinθ,三力合力为零,则由平行四边形法则:
F=
=9N
由正弦定理得:
=
故α=90°
即F与AC垂直.故C正确,A、B、D错误.
故选C.
重力沿斜面向下的分量:mgsinθ=15(N)
在斜面这一平面内,f、F与重力沿斜面向下的分量mgsinθ,三力合力为零,则由平行四边形法则:
F=
| (mgsinθ)2+f2-2mgsinθ?f?cos143° |
由正弦定理得:
| F |
| sin37° |
| mgsinθ |
| sinα |
故α=90°
即F与AC垂直.故C正确,A、B、D错误.
故选C.
点评:本题中物体受力不在同一平面内,而是分布立体空间,将所有的力分为两个平面进行研究,在任何一平面内物体的合力都为零.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
如图所示,楔形斜面体倾角为37°,其BC长为0.8m,AB宽为0.6m,一重为25N的木块原先在斜面体上部,它与斜面间的动摩擦因数为0.6,要使木块沿对角线AC方向匀速下滑,(sin37°=0.6,cos37°=0.8),需要对它施加方向平行于斜面的力F,则F的大小和方向为( )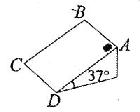
| A.15N沿斜面向上 |
| B.15N与AB边平行 |
| C.9N近似于沿DB方向 |
| D.9N近似于沿CA方向 |

