题目内容
8.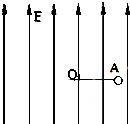 如图所示,空间存在着电场强度为E=2.5×103N/C、方向竖直向上的匀强电场,一长为L=0.5m的绝缘细线,一端固定在O点,一端拴着质量m=5×10-3kg、电荷量q=4×10-5C的小球.现将细线拉直到水平位置A,使小球由A静止释放,则小球能运动到最高点.不计阻力.取g=10m/s2.求:
如图所示,空间存在着电场强度为E=2.5×103N/C、方向竖直向上的匀强电场,一长为L=0.5m的绝缘细线,一端固定在O点,一端拴着质量m=5×10-3kg、电荷量q=4×10-5C的小球.现将细线拉直到水平位置A,使小球由A静止释放,则小球能运动到最高点.不计阻力.取g=10m/s2.求:(1)小球的电性.
(2)细线在最高点受到的拉力.
(3)若小球刚好运动到最高点时细线断裂,则细线断裂后小球继续运动到与O点水平方向距离为细线的长度L时,小球距OA所在水平面的高度.
分析 (1)由带电小球在电场力作用下,运动到最高点并拉断细线,则可判定电场力方向,再由电场强度方向可确定小球的电性.
(2)小球从释放到最高点,由动能定理可求出动能的变化,再由牛顿第二定律可得拉力大小.
(3)当细线断裂后,小球做类平抛运动,则将此运动分解成水平方向匀速运动与竖直方向匀加速运动,从而求出小球距O点的高度.
解答 解:(1)由小球运动到最高点,说明电场力竖直向上,再由电场线竖直向上,则可判定小球带正电.
(2)设小球运动到最高点时速度为v,对该过程由动能定理有:
(qE-mg)L=$\frac{1}{2}$mv2-0…①
在最高点对小球由牛顿第二定律得:
T+mg-qE=m$\frac{{v}^{2}}{L}$…②
由①②式解得:T=15N;
(3)小球在细线断裂后,在竖直方向的加速度设为a,由牛顿第二定律得:a=$\frac{qE-mg}{m}$…③
设小球在水平方向运动L的过程中,历时t,则 L=vt…④
设竖直方向上的位移为s,则 s=$\frac{1}{2}$at2…⑤
由①③④⑤解得:s=0.125m
小球距O点高度为:s+L=0.625m.
答:(1)小球的电性为正电.
(2)细线能承受的最大拉力为15N
(3)当小球继续运动后与O点水平方向距离为L时,小球距O点的高度0.625m.
点评 小球由静止释放,当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂.从而可求出此时的速度,这是本题的突破口.并值得注意是细线断裂后,速度与合力相垂直,且合力恒定,所以做类平抛运动.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
18.试判断下面的几个速度中是瞬时速度是( )
| A. | 物体在第1秒内的速度是4m/s | |
| B. | 物体在第2秒末的速度是4m/s | |
| C. | 物体在通过其路径上某一点的速度是4m/s | |
| D. | 物体在通过某一段位移时的速度是4m/s |
19.枪管呈水平状态对准小球,枪口与小球之间的距离为100m,当子弹射出枪口时,小球恰好开始自由落下.小球落下0.2s时被子弹击中,则子弹离开枪口时的速度为(取g=10m/s2)( )
| A. | 200m/s | B. | 300m/s | C. | 400m/s | D. | 500m/s |
16.如图所示电路中,L为电感线圈,线圈电阻不计,A、B为两灯泡,则不正确的是( )
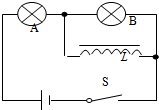

| A. | 合上S时,A先亮,B后亮 | B. | 合上S时,A、B同时亮起来 | ||
| C. | 合上S过一会儿后,A继续亮,B熄灭 | D. | 断开S时,A熄灭,B闪亮一下再熄灭 |
13.一质量为0.5kg的物体,从10m高处以6m/s的水平速度抛出(不计空气阻力),在0.8s末(尚未落地)重力的瞬时功率为(g取10m/s2)( )
| A. | 20W | B. | 30W | C. | 40W | D. | 50W |
20. 如图所示,A、B、O、C为同一竖直平面内的四点,其中A、B、O沿同一竖直线,B、C同在以O为圆心的圆周(用虚线表示)上,沿AC方向固定有一光滑绝缘细杆L,在O点固定放置一带负电的小球.现有两个质量和电荷量都相同的带正电的小球a、b,先将a穿在细杆上,让其从A点由静止开始沿杆下滑;后使b从A点由静止开始沿竖直方向下落.各带电小球均可视为点电荷,则下列说法中正确的是( )
如图所示,A、B、O、C为同一竖直平面内的四点,其中A、B、O沿同一竖直线,B、C同在以O为圆心的圆周(用虚线表示)上,沿AC方向固定有一光滑绝缘细杆L,在O点固定放置一带负电的小球.现有两个质量和电荷量都相同的带正电的小球a、b,先将a穿在细杆上,让其从A点由静止开始沿杆下滑;后使b从A点由静止开始沿竖直方向下落.各带电小球均可视为点电荷,则下列说法中正确的是( )
 如图所示,A、B、O、C为同一竖直平面内的四点,其中A、B、O沿同一竖直线,B、C同在以O为圆心的圆周(用虚线表示)上,沿AC方向固定有一光滑绝缘细杆L,在O点固定放置一带负电的小球.现有两个质量和电荷量都相同的带正电的小球a、b,先将a穿在细杆上,让其从A点由静止开始沿杆下滑;后使b从A点由静止开始沿竖直方向下落.各带电小球均可视为点电荷,则下列说法中正确的是( )
如图所示,A、B、O、C为同一竖直平面内的四点,其中A、B、O沿同一竖直线,B、C同在以O为圆心的圆周(用虚线表示)上,沿AC方向固定有一光滑绝缘细杆L,在O点固定放置一带负电的小球.现有两个质量和电荷量都相同的带正电的小球a、b,先将a穿在细杆上,让其从A点由静止开始沿杆下滑;后使b从A点由静止开始沿竖直方向下落.各带电小球均可视为点电荷,则下列说法中正确的是( )| A. | 从A点到C点,小球a做匀加速运动 | |
| B. | 从A点到C点,小球a的机械能先增大后减小,但机械能与电势能之和不变 | |
| C. | 小球a经过C点时的动能大于小球b经过B点时的动能 | |
| D. | 小球a从A点到C点的过程中电场力做的功等于小球b从A点到B点的过程中电场力做的功 |
17.质量为m的物体,在距地面h高处以$\frac{g}{3}$的加速度由静止竖直下落到地面,下列说法中错误的是( )
| A. | 重力做功mgh | B. | 物体的机械能减少$\frac{2mgh}{3}$ | ||
| C. | 物体的动能增加$\frac{mgh}{3}$ | D. | 物体的重力势能减少$\frac{mgh}{3}$ |
18.通常一次闪电过程历时约0.2~0.3s,它由若干个相继发生的闪击构成.每个闪击持续时间仅40~80μs,电荷转移主要发生在第一个闪击过程中.在某一次闪电前云地之间的电势差约为1.0×109V,云地间距离约为l km;第一个闪击过程中云地间转移的电荷量约为7C,闪击持续时间约为70μs.假定闪电前云地间的电场是均匀的.根据以上数据,下列判断正确的是( )
| A. | 闪电电流的瞬时值可达到1×106A | |
| B. | 整个闪电过程的平均功率小于l×1014W | |
| C. | 闪电前云地间的电场强度约为l×106V/m | |
| D. | 整个闪电过程向外释放的能量约为7×109J |