题目内容
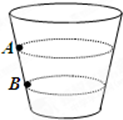杂技表演“飞车走壁”的演员骑着摩托车飞驶在光滑的圆锥形筒壁上，筒的轴线垂直于水平面，圆锥筒固定不动，演员和摩托车的总质量为m，先后在A、B两处紧贴着内壁分别在图中虚线所示的水平面内做匀速圆周运动，则以下说法中不正确的是（ ）分析：演员和摩托车受重力和支持力，靠重力和支持力的合力提供圆周运动的向心力，根据合力提供向心力比较线速度、角速度的大小，根据平行四边形定则比较支持力的大小和合力的大小．
解答：解：重力不变，支持力方向相同，根据力的合成，知在A、B两处两支持力大小、合力大小相等．根据F合=m
=mrω2得，v=
，ω=
，知半径越大，线速度越大，角速度越小．所以A处的线速度大于B处的线速度，A处的角速度小于B处的角速度．故A、B、D正确，C错误．
本题选错误的，故选C．
| v2 |
| r |
|
|
本题选错误的，故选C．
点评：解决本题的关键知道向心力的来源，运用牛顿第二定律进行求解．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
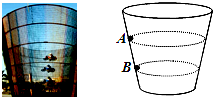杂技表演“飞车走壁”的演员骑着摩托车飞驶在光滑的圆锥形筒壁上，筒的轴线垂直于水平面，圆锥筒固定不动，演员和摩托车的总质量为m，先后在A、B两处紧贴着内壁分别在图中虚线所示的水平面内做匀速圆周运动，则（ ）
