Question

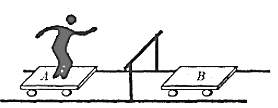
【题目】平板车上的跨栏运动如图所示，光滑水平地面上人与滑板A一起以v0=0.5m/s的速度前进，正前方不远处有一距离轨道高h=0.7875m高的（不考虑滑板的高度）横杆，横杆另一侧有一静止滑板B，当人与A行至横杆前，人相对滑板竖直向上起跳越过横杆，A从横杆下方通并与B发生弹性碰撞，之后人刚好落到B上，不计空气阻力，已知m人=40 kg.mA=5 kg.mB=10 kg.g取l0m/s2,求：

（1）人跳离滑板A的最小速度（相对地面）：

（2）最终人与B的共同速度。

Answer 1

【答案】（1）（2）m/s

【解析】(1)人起跑的竖直速度至少为vy2=2gh=15.75m2/s2.

因为相对板A的水平速度相同，所以

(2)人跳起后A与B碰撞前后动量守恒，机械能守恒，设碰后A的速度v1，B的速度为v2，

解得：v1=-m/s, v1=m/s

人下落与B作用前后，水平方向动量守恒，设共同速度v0，m人v0+mBv2=（m人十mB）v3

代入数据得