题目内容
4.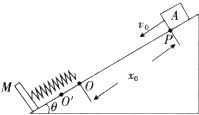 如图所示,倾角为θ的固定斜面的底端有一挡板M,轻弹簧的下端固定在挡板M上,在自然长度下,弹簧的上端在O位置.质量为m的物块A(可视为质点)从P点以初速度v0沿斜面向下运动,PO=x0,物块A与弹簧接触后将弹簧上端压到O'点位置,然后A被弹簧弹回.A离开弹簧后,恰好能回到P点.已知A与斜面间的动摩擦因数为μ,重力加速度用g表示.求:
如图所示,倾角为θ的固定斜面的底端有一挡板M,轻弹簧的下端固定在挡板M上,在自然长度下,弹簧的上端在O位置.质量为m的物块A(可视为质点)从P点以初速度v0沿斜面向下运动,PO=x0,物块A与弹簧接触后将弹簧上端压到O'点位置,然后A被弹簧弹回.A离开弹簧后,恰好能回到P点.已知A与斜面间的动摩擦因数为μ,重力加速度用g表示.求:(1)物块A运动到O点的速度大小;
(2)O点和O'点间的距离x1.
分析 (1)对从P到O过程,运用动能定理列式求解即可;
(2)对从P到返回P的整个过程,运用动能定理列式求解即可.
解答 解:(1)对从P点到O点的过程,根据动能定理,有:
mgsinθ•x0-μmgcosθ•x0=$\frac{1}{2}$mv2-$\frac{1}{2}m{v}_{0}^{2}$
解得:物块A运动到O点的速度大小为:v=$\sqrt{{v}_{0}^{2}+2g(sinθ-μcosθ){x}_{0}}$
(2)物块从P向下再到返回P的整个过程,根据动能定理,有:
-μmgcosθ•2(x0+x1)=0-$\frac{1}{2}m{v}_{0}^{2}$
解得:x1=$\frac{{v}_{0}^{2}}{4μgcosθ}$-x0;
答:(1)物块A运动到O点的速度大小是$\sqrt{{v}_{0}^{2}+2g(sinθ-μcosθ){x}_{0}}$;
(2)O点和O'点间的距离x1是$\frac{{v}_{0}^{2}}{4μgcosθ}$-x0.
点评 本题关键灵活选择过程,多次根据动能定理和功能关系列式求解,注意重力和弹力做功与路径无关,摩擦力做功与路径有关.

练习册系列答案
相关题目
15. 如图所示,一质量为m的物体,从倾角为θ的光滑斜面顶端由静止下滑,开始下滑时离地高度为h,下列说法正确的是( )
如图所示,一质量为m的物体,从倾角为θ的光滑斜面顶端由静止下滑,开始下滑时离地高度为h,下列说法正确的是( )
 如图所示,一质量为m的物体,从倾角为θ的光滑斜面顶端由静止下滑,开始下滑时离地高度为h,下列说法正确的是( )
如图所示,一质量为m的物体,从倾角为θ的光滑斜面顶端由静止下滑,开始下滑时离地高度为h,下列说法正确的是( )| A. | 当物体滑至斜面底端时重力的瞬时功率为mg$\sqrt{2gh}$•sinθ | |
| B. | 当物体滑至斜面底端时重力的瞬时功率为mg$\sqrt{2gh}$ | |
| C. | 物体下滑过程中重力的平均功率为mg$\sqrt{2gh}$•sinθ | |
| D. | 物体下滑过程中重力的平均功率为 $\frac{1}{2}$mg$\sqrt{2gh}$•sinθ |
13.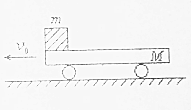 如图所示,在光滑的水平地面上,质量为M、足够长的小平板车以速度v向左匀速运动,一质量为m的物块被无初速度地放到车的左端,由于摩擦力的作用,物块也运动起来,已知动摩擦因数为μ,当物块达到最大速度时( )
如图所示,在光滑的水平地面上,质量为M、足够长的小平板车以速度v向左匀速运动,一质量为m的物块被无初速度地放到车的左端,由于摩擦力的作用,物块也运动起来,已知动摩擦因数为μ,当物块达到最大速度时( )
 如图所示,在光滑的水平地面上,质量为M、足够长的小平板车以速度v向左匀速运动,一质量为m的物块被无初速度地放到车的左端,由于摩擦力的作用,物块也运动起来,已知动摩擦因数为μ,当物块达到最大速度时( )
如图所示,在光滑的水平地面上,质量为M、足够长的小平板车以速度v向左匀速运动,一质量为m的物块被无初速度地放到车的左端,由于摩擦力的作用,物块也运动起来,已知动摩擦因数为μ,当物块达到最大速度时( )| A. | 平板车的速度最小 | |
| B. | 此过程中M和m组成的系统所受摩擦力冲量为零 | |
| C. | 此过程中摩擦力对系统做功为零 | |
| D. | 经历此过程后,m所受合外力的冲量为零 |
20. 如图甲,某电场的一条电场线与Ox轴重合,电场中x坐标上电势随位置x变化的图象如图乙所示(曲线的斜率为电场强度大小),如果有一电荷在x2处由静止释放,电荷仅受电场力的作用,则电荷运动到坐标原点的过程中( )
如图甲,某电场的一条电场线与Ox轴重合,电场中x坐标上电势随位置x变化的图象如图乙所示(曲线的斜率为电场强度大小),如果有一电荷在x2处由静止释放,电荷仅受电场力的作用,则电荷运动到坐标原点的过程中( )
 如图甲,某电场的一条电场线与Ox轴重合,电场中x坐标上电势随位置x变化的图象如图乙所示(曲线的斜率为电场强度大小),如果有一电荷在x2处由静止释放,电荷仅受电场力的作用,则电荷运动到坐标原点的过程中( )
如图甲,某电场的一条电场线与Ox轴重合,电场中x坐标上电势随位置x变化的图象如图乙所示(曲线的斜率为电场强度大小),如果有一电荷在x2处由静止释放,电荷仅受电场力的作用,则电荷运动到坐标原点的过程中( )| A. | 加速度越来越小 | B. | 电势能越来越大 | ||
| C. | 动能先增大后减小 | D. | 电场力做功的功率越来越大 |
9.上海锦江乐园新建的“摩天转轮”,它的直径达98m,世界排名第五.游人乘坐时,转轮始终不停地匀速转动,每转一周用时25min,下列说法中正确的是( )
| A. | 乘客在乘坐过程中对座位的压力始终不变 | |
| B. | 乘客运动的加速度始终保持不变 | |
| C. | 每个乘客都在做加速度为零的匀速运动 | |
| D. | 每时每刻,每个乘客受到的合力都不等于零 |
16.质点作直线运动的v-t图象如图所示,则( )
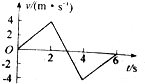

| A. | 6s内物体运动的平均速率为零 | |
| B. | 6s内物体运动的平均速度为零 | |
| C. | 2-4s内的位移为零,路程为4m | |
| D. | 0-2s内的加速度为4-6s内的加速度方向相反,大小相等 |
14.光电效应实验中,下列表述正确的是( )
| A. | 光照时间越长光电流越大 | |
| B. | 入射光频率低于金属板的极限频率不能有光电子逸出 | |
| C. | 遏止电压与入射光的频率有关 | |
| D. | 入射光足够强就可以有光电流 |
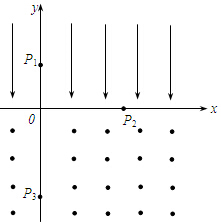 如图所示,在y>0的空间中存在匀强电场,场强沿y轴负方向;在y<0的空间中,存在匀强磁场,磁场方向垂直xy平面(纸面)向外.一电量为q、质量为m的带正电的运动粒子,经过y轴上y=h处的点P1时速度为v0,方向沿x轴正方向;然后,经过x轴上x=2h处的P2点进入磁场,并经过y轴上y=-2h处的P3点.不计重力.求:
如图所示,在y>0的空间中存在匀强电场,场强沿y轴负方向;在y<0的空间中,存在匀强磁场,磁场方向垂直xy平面(纸面)向外.一电量为q、质量为m的带正电的运动粒子,经过y轴上y=h处的点P1时速度为v0,方向沿x轴正方向;然后,经过x轴上x=2h处的P2点进入磁场,并经过y轴上y=-2h处的P3点.不计重力.求: