��Ŀ����
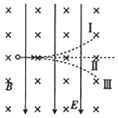
����Ŀ���ɴ����زշ��ع���һ��ɼ�Ϊ���¹��̣��ڸ߿գ������dz�ϡ�����ɲ����ǿ�������������ֱ�������Ϊ���ٶ�Ϊ����ȼ���ֱ���˶����ڷ��ز��½��������һ���{��ʱ�������������ɺ��ԣ�����Ϊ���ٶ���С�ļ����˶���Ȼ����������ľ���Ϊh���˺������������������Ϊ�ȼ���ֱ���˶���ʹ��ƽ�Ƚ��䵽���棬�������ʱ���ٶ�Ϊ0���ù���������ʱ��Ϊt����֪���ز��ȼ������������������С���ٶȴ�С�Ĺ�ϵ�ɱ�ʾΪf=kv2�����زյ�����Ϊm�������Ƿ��زս�������������ı仯���������ٶ�ʼ��Ϊg����
��1�����ز����������ٶȺ�������������п˷������������Ĺ���
��2�����زշ������������������������ĺ�����С��
���𰸡���1��![]() �� mgh����2��
�� mgh����2��![]()
����������1�����ز���������У�����Ϊ�㣬�ٶ�������� mg=kvm2��
�ɵ÷��ز����������ٶ� vm=![]()
������������п˷������������Ĺ���W=kvm2h=mgh��
��2����������������زռ����˶��ļ��ٶȴ�СΪ
a=![]() =
=![]()
����ţ�ٵڶ����ɵ� F��mg=ma
�ɵã����زշ������������������������ĺ�����С F=mg+m![]() ��
��

 ��˼ά������ҵϵ�д�
��˼ά������ҵϵ�д�����Ŀ��ijͬѧ���С���ݵķ����������ߣ�ʵ�������У�
��ѹ��������Ϊ3V������Ϊ3k��
������������Ϊ0.6A������ԼΪ2��
��ֵ����R0����ֵΪ1k��
С����L�����ѹΪ3.8 V
����������R����ֵ��ΧΪ010��
���E���綯��Ϊ6V
����S���������ɣ�

��ͬѧ����ͼ����ʾ�ĵ�·ͼ����ʵ�飬ͨ����ȷʵ������Ͷ������õ���һ���ѹ����ʾ���͵�������ʾ���������������±���
������A�� | 0.085 | 0.155 | 0.212 | 0.235 | 0.278 | 0.315 |
��ѹ��V�� | 0.17 | 0.60 | 1.20 | 1.50 | 2.10 | 2.70 |
��1������ѹ��ʾ��Ϊ1.20 Vʱ��С�������˵ĵ�ѹΪ__V����������λ��Ч���֣�
��2����ͼ���л���С���ݵķ�����������_______��
��3���������С������綯��Ϊ3V������Ϊ10���ĸɵ�����ӳɱպϵ�·����ʱС���ݵĵ���Ϊ__����ʵ�ʹ���Ϊ__W�������������λ��Ч���֣�