题目内容
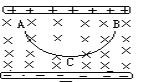
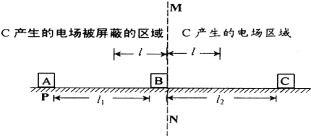
【题目】在粗糙绝缘的水平面上的同一直线上有A、B、C三个质量都为m的物体（都可视为质点），其中物体C被固定，其带电量为+Q，它产生的电场在竖直面MN的左侧被屏蔽。物体B带电量为+q，恰好处在被屏蔽区边缘；物体A不带电。此时A、B均静止，它们相距l1，B与C相距l2。现对位于P点的物体A施加一水平向右的瞬时冲量，A在向右运动过程中与B碰撞后粘连（碰撞时间极短），并进入电场区前进了l（l＜l2）的距离时，由于物体C排斥作用而折回，再次进入被屏蔽区后恰好也前进了l距离时静止。已知物体A、B与整个水平面间的动摩擦因数都为μ，求：最初在P点时对物体A施加的瞬时冲量的大小。（竖直面MN不影响物体在两区域间穿行，忽略带电体在MN左侧被屏蔽区域受到的一切电场力）
【答案】
【解析】
对A由动量定理知
I=mv0-0
A和B碰撞前，对A由动能定理知：
μmgl1=
mv12-mv02
A和B碰撞过程动量守恒：
mv1=2mv2
从A和 B碰撞到静止的全过程，由动能定理知：
μ2mg3l=02m v22
联立解得：
练习册系列答案
相关题目
