Question

【题目】如图所示，A、B为两颗在不同轨道上绕地球做匀速圆周运的卫星，A的轨道半径大于B的轨道半径，用vA、vB分别表示A、B线速度大小，用TA、TB表示A、B卫星的周期，aA、aB表示向心加速度大小，FA、FB表示其万有引力大小，ωA、ωB表示其角速度大小，则正确的是

A.vA < vB、aA < aB、ωA < ωB、FA < FB

B.vA < vB、aA < aB、TA > TB

C.TA > TB、vA < vB、FA = FB

D.TA < TB、FA > FB、aA > aB

Answer 1

【答案】B

【解析】

ABCD．卫星绕地球做匀速圆周运动，万有引力提供向心力，则

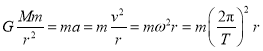
解得

，，，

由上述计算结果可知，轨道半径r越大，加速度a、线速度v、角速度都越小，只有周期T越大。因为rA > rB，所以aA < aB、vA < vB、ωA < ωB、TA > TB，又因为A、B卫星的质量大小关系未知，所以A、B卫星的万有引力FA、FB的大小无法比较，故B正确，ACD错误。

故选B。