题目内容
（12分）如图所示，在水平方向的匀强电场中，一不可伸长的不导电的细线的一端连接着一个质量为m的带电小球，另一端固定在O点，把小球拉起至细线与场强平行，然后无初速度释放，小球摆动到最低点的另一侧，线与竖直方向的最大夹角为θ，求小球经过最低点时细线对小球的拉力。
解析：带电小球在运动过程中，只有重力和电场力做功，因此小球的电势能与机械能守恒，也可以用动能定理求得电场力做功和重力做功的数值关系，进而可以求出小球在最低点时的速度。
正确解答：小球运动到最低点时，小球受到的重力和电场力的合力是小球的向心力，设细线长度为L，由牛顿第二定律有：
……①
小球从开始运动到左边最大位置，由动能定理有：
……②
从开始到最低点由动能定理有：
……③
解得：
……④
练习册系列答案
相关题目
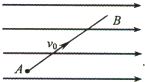如图所示，在水平方向的匀强电场中，一初速度为v0的带电微粒沿着竖直平面内的直线由A点运动到B点的过程中，微粒的（ ）| A、电势能一定减少，动能一定减少 | B、电势能一定增加，动能一定增加 | C、电势能一定减少，动能一定增加 | D、电势能一定增加，动能一定减少 |
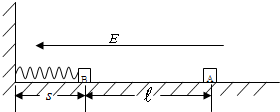（2008?揭阳二模）在绝缘水平面上，放一质量为m=2.0×10-3kg的带正电滑块A，所带电量为q=1.0×10-7C，在滑块A的左边?处放置一个不带电、质量M=4.0×10-3kg的绝缘滑块B，B的左端接触（不连接）于固定在竖直墙壁的轻弹簧上，轻弹簧处于自然状态，弹簧原长s=0.05m，如图所示．在水平方向加一水平向左的匀强电场，电场强度的大小为E=4.0×105N/C，滑块A由静止释放后向左滑动并与滑块B发生碰撞，设碰撞时间极短，碰撞后结合在一起共同运动的速度为v=1m/s，两物体一起压缩弹簧至最短处（弹性限度内）时，弹簧的弹性势能E0=3.2×10-3J．设两滑块体积大小不计，与水平面间的动摩擦因数为μ=0.50，摩擦不起电，碰撞不失电，g取10m/s2．求：
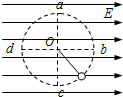（2009?南通模拟）如图所示，在水平方向的匀强电场中，绝缘细线的一端固定在O点，另一端系一带正电的小球在竖直平面内做圆周运动，小球所受电场力大小等于重力大小．则（ ）
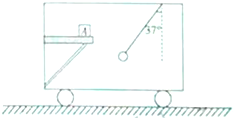如图所示，在水平方向上加速前进的车厢中，挂着小球的悬线与竖直方向成37°角，放在车厢里的水平桌面上的物体A相对桌面静止不动，若A的质量为1.0kg，取g=10m/s2，sin37°=0.6，cos37°=0.8．求：