Question

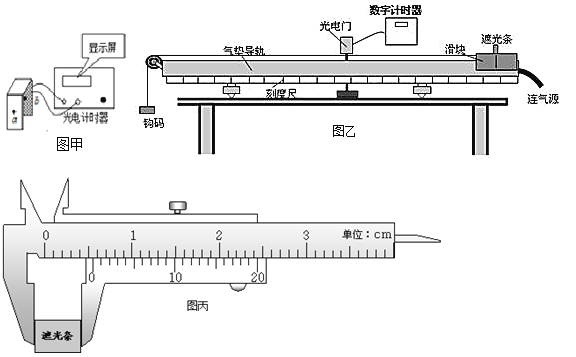
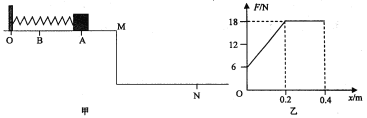
【题目】如图甲所示，在距离地面高度为h＝0．80 m的平台上有一轻质弹簧，其左端固定于竖直挡板上，右端与质量m＝0．50 kg、可看作质点的物块相接触（不粘连），OA段粗糙且长度等于弹簧原长，其余位置均无阻力作用。物块开始静止于A点，与OA段的动摩擦因数μ＝0．50。现对物块施加一个水平向左的外力F，大小随位移x变化关系如图乙所示。物块向左运动x＝0．40 m到达B点，到达B点时速度为零，随即撤去外力F，物块在弹簧弹力作用下向右运动，从M点离开平台，落到地面上N点，取g＝10 m／s2,则（ ）

A．弹簧被压缩过程中外力F做的功为6．0 J

B．弹簧被压缩过程中具有的最大弹性势能为6．0J

C．整个运动过程中克服摩擦力做功为4．0J

D．MN的水平距离为1．6 m

Answer 1

【答案】AD

【解析】

试题分析：根据F-x图象与坐标轴所围的面积表示力F做的功，则弹簧被压缩过程中外力F做的功为 WF=

×0．2+18×0．2=6．0J．故A正确．物块向左运动的过程中，克服摩擦力做功 Wf=μmgx=0．5×0．5×10×0．4J=1．0J；根据能量守恒可知，弹簧被压缩过程中具有的最大弹性势能为 Ep=WF-Wf=5．0J，故B错误．整个运动过程中克服摩擦力做功为 Wf总=2μmgx=2．0J．故C错误．设物块离开M点时的速度为v．对整个过程，由能量守恒得：mv2=WF-Wf总，解得 v=4m/s；物块离开M点后做平抛运动，则有h=gt2；x=vt，解得 x=1．6m．故D正确．故选AD。