题目内容
 (2008?滨州二模)如图所示的竖直平面内有范围足够大、水平向左的匀强电场,在虚线的左侧有垂直纸面向里的匀强磁场,磁感强度大小为B,一绝缘轨道由两段直杆和一半径为R的半圆环组成,固定在纸面所在的竖直平面内,PQ、MN水平且足够长,半圆环MAP在磁场边界左侧,P、M点在磁场边界线上,NMAP段光滑,PQ段粗糙.现在有一质量为m、带电荷量为+q的小环套在MN杆上,它所受电场力为重力的
(2008?滨州二模)如图所示的竖直平面内有范围足够大、水平向左的匀强电场,在虚线的左侧有垂直纸面向里的匀强磁场,磁感强度大小为B,一绝缘轨道由两段直杆和一半径为R的半圆环组成,固定在纸面所在的竖直平面内,PQ、MN水平且足够长,半圆环MAP在磁场边界左侧,P、M点在磁场边界线上,NMAP段光滑,PQ段粗糙.现在有一质量为m、带电荷量为+q的小环套在MN杆上,它所受电场力为重力的| 3 | 4 |
(1)求DM间距离x0;
(2)求上述过程中小环第一次通过与O等高的A点时半圆环对小环作用力的大小;
(3)若小环与PQ间动摩擦因数为μ(设最大静摩擦力与滑动摩擦力大小相等),现将小环移至M点右侧4R处由静止开始释放,求小环在整个运动过程中克服摩擦力所做的功.
分析:(1)小环刚好到达P点时速度为零,对D到P为研究过程,运用动能定理求出DM间的距离.
(2)对D到A为研究过程,运用动能定理求出A点的速度,根据牛顿第二定律,沿半径方向上合力提供向心力,求出弯杆对小环作用力的大小.
(3)需讨论摩擦力的大小与电场力的大小关系,若摩擦力大于电场力,则运动到P点右侧停止;若摩擦力小于电场力,则环最终在DP间往复运动.根据动能定理求出摩擦力做的功.
(2)对D到A为研究过程,运用动能定理求出A点的速度,根据牛顿第二定律,沿半径方向上合力提供向心力,求出弯杆对小环作用力的大小.
(3)需讨论摩擦力的大小与电场力的大小关系,若摩擦力大于电场力,则运动到P点右侧停止;若摩擦力小于电场力,则环最终在DP间往复运动.根据动能定理求出摩擦力做的功.
解答:解:(1)小环刚好到达P点时速度vP=0,由动能定理得
qEx0-2mgR=0
而 qE=
所以x0=
(2)设小环在A点时的速度为vA,由动能定理得
qE(x0+R)-mgR=
m
-0
因此vA=
设小环在A点时所受半圆环轨道的作用力大小为N,由牛顿第二定律得
N-qvAB-qE=m
解得 N=
+
(3)若f=μmg≥qE,即μ≥
.小环第一次到达P点右侧s1距离处静止,由动能定理得
qE(4R-s1)-2mgR-fs1=0
而f=μmg,因此得 s1=
设克服摩擦力所做的功为W,则 W=fs1=
若f=μmg≤qE,即μ<
.环经过来回往复运动,最后只能在PD之间往复运动,设克服摩擦力所做的功为W,则
qE(4R)-mg(2R)-W=0
解得W=mgR
答:(1)DM间距离x0是
.
(2)上述过程中小环第一次通过与O等高的A点时半圆环对小环作用力的大小是
+
;
(3)小环在整个运动过程中克服摩擦力所做的功为
或mgR.
qEx0-2mgR=0
而 qE=
| 3mg |
| 4 |
所以x0=
| 8R |
| 3 |
(2)设小环在A点时的速度为vA,由动能定理得
qE(x0+R)-mgR=
| 1 |
| 2 |
| v | 2 A |
因此vA=
| ||
| 2 |
设小环在A点时所受半圆环轨道的作用力大小为N,由牛顿第二定律得
N-qvAB-qE=m
| ||
| R |
解得 N=
| 17mg |
| 4 |
qB
| ||
| 2 |
(3)若f=μmg≥qE,即μ≥
| 3 |
| 4 |
qE(4R-s1)-2mgR-fs1=0
而f=μmg,因此得 s1=
| 4R |
| 4μ+3 |
设克服摩擦力所做的功为W,则 W=fs1=
| 4μmgR |
| 4μ+3 |
若f=μmg≤qE,即μ<
| 3 |
| 4 |
qE(4R)-mg(2R)-W=0
解得W=mgR
答:(1)DM间距离x0是
| 8R |
| 3 |
(2)上述过程中小环第一次通过与O等高的A点时半圆环对小环作用力的大小是
| 17mg |
| 4 |
qB
| ||
| 2 |
(3)小环在整个运动过程中克服摩擦力所做的功为
| 4μmgR |
| 4μ+3 |
点评:运用动能定理解题需合适地选取研究的过程,根据动能定理列出表达式求解.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目

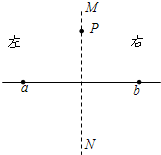 (2008?滨州二模)图中a、b是两个点电荷,它们的电量分别为Q1、Q2,MN是ab连线的中垂线,P是中垂线上的一点.下列哪种情况能使P点场强方向指向MN的左侧?( )
(2008?滨州二模)图中a、b是两个点电荷,它们的电量分别为Q1、Q2,MN是ab连线的中垂线,P是中垂线上的一点.下列哪种情况能使P点场强方向指向MN的左侧?( ) (2008?滨州二模)一同学用如图所示装置研究一定质量气体的压强与体积的关系,实验过程中温度保持不变,最初,U形管两臂中的水银面齐平,烧瓶中无水,当用注射器往烧瓶中注入水时,U形管两臂中的水银面出现高度差,实验的部分数据记录在下表.
(2008?滨州二模)一同学用如图所示装置研究一定质量气体的压强与体积的关系,实验过程中温度保持不变,最初,U形管两臂中的水银面齐平,烧瓶中无水,当用注射器往烧瓶中注入水时,U形管两臂中的水银面出现高度差,实验的部分数据记录在下表. (2008?滨州二模)如图所示,水平地面上固定着一竖直立柱,某人通过柱顶的定滑轮将200N的重物拉住不动,已知人拉着绳的一端,绳与水平地面夹角为30°,则定滑轮所受的压力大小为( )
(2008?滨州二模)如图所示,水平地面上固定着一竖直立柱,某人通过柱顶的定滑轮将200N的重物拉住不动,已知人拉着绳的一端,绳与水平地面夹角为30°,则定滑轮所受的压力大小为( )