题目内容
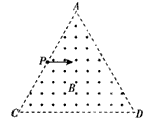
 如图所示,在边长为
如图所示,在边长为| 3 |
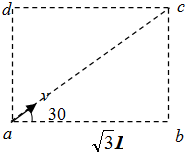
分析:根据粒子的运动的轨迹的情况,画出粒子运动的轨迹,找出粒子运动的轨迹所对应的圆心角的大小可以求得粒子的运动的时间.要从c点射出,应有qE=Bqv.
解答:解:粒子从d点射出运动的轨迹如图,在磁场中偏转120°
据题意有t=
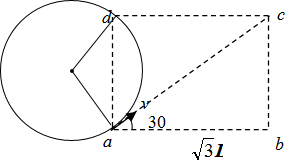
带电粒子的洛伦兹力提供向心力得:qvB=
得:R=
又:T=
=
由轨迹图可得:粒子圆周运动半径R=
=
所以:v=
要从c点射出,应有qE=Bqv
联立以上各式,得电场强度大小为E=Bv=
,方向垂直于ac向下.
答:电场强度的大小为
,方向垂直于ac向下.
据题意有t=
| T |
| 3 |

带电粒子的洛伦兹力提供向心力得:qvB=
| mv2 |
| R |
得:R=
| mv |
| qB |
又:T=
| 2πR |
| v |
| 2πm |
| qB |
由轨迹图可得:粒子圆周运动半径R=
| ||
| sin60° |
| ||
| 3 |
所以:v=
| ||
| 3m |
要从c点射出,应有qE=Bqv
联立以上各式,得电场强度大小为E=Bv=
4
| ||
| 27qt2 |
答:电场强度的大小为
4
| ||
| 27qt2 |
点评:根据粒子的运动的轨迹的情况,找出粒子运动的轨迹所对应的圆心角的大小可以求得粒子的运动的时间.

练习册系列答案
相关题目
 (A)如图所示,在边长为L=1m的等边三角形ACD区域内,存在磁感应强度为B=
(A)如图所示,在边长为L=1m的等边三角形ACD区域内,存在磁感应强度为B= 如图所示,在边长为l的正方形区域内,有与y轴平行的匀强电场和垂直于纸面的匀强磁场.一个带电粒子(不计重力)从原点O沿x轴进入场区,恰好做匀速直线运动,穿过场区的时间为T0;若撤去磁场,只保留电场,其他条件不变,该带电粒子穿过场区的时间为
如图所示,在边长为l的正方形区域内,有与y轴平行的匀强电场和垂直于纸面的匀强磁场.一个带电粒子(不计重力)从原点O沿x轴进入场区,恰好做匀速直线运动,穿过场区的时间为T0;若撤去磁场,只保留电场,其他条件不变,该带电粒子穿过场区的时间为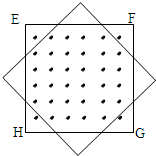 如图所示,在边长为a的正方形区域内有匀强磁场,磁感应强度为B,其方向垂直纸面向外,一个边长也为a的正方形形导线框架EFGH正好与上述磁场区域的边界重合,现使导线框以周期T绕其中心O点在纸面内匀速转动,经过
如图所示,在边长为a的正方形区域内有匀强磁场,磁感应强度为B,其方向垂直纸面向外,一个边长也为a的正方形形导线框架EFGH正好与上述磁场区域的边界重合,现使导线框以周期T绕其中心O点在纸面内匀速转动,经过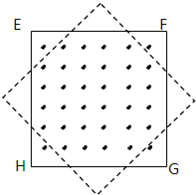 如图所示,在边长为a的正方形区域内有匀强磁场,磁感应强度为B,其方向垂直纸面向外,一个边长也为a的单匝正方形导线框架EFGH正好与上述磁场区域的边界重合,导线框的电阻为R.现使导线框以周期T绕其中心O点在纸面内匀速转动,经过八分之一T 导线框转到图中虚线位置,则在这八分之一T 时间内( )
如图所示,在边长为a的正方形区域内有匀强磁场,磁感应强度为B,其方向垂直纸面向外,一个边长也为a的单匝正方形导线框架EFGH正好与上述磁场区域的边界重合,导线框的电阻为R.现使导线框以周期T绕其中心O点在纸面内匀速转动,经过八分之一T 导线框转到图中虚线位置,则在这八分之一T 时间内( )