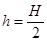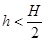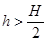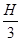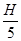题目内容
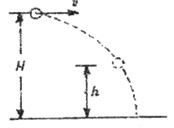
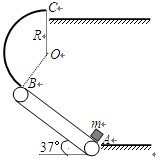
(11分)长为6L、质量为6m的匀质绳,置于特制的水平桌面上,绳的一端悬垂于桌边外,另一端系有一个可视为质点的质量为M的木块,如图所示。木块在AB段与桌面无摩擦,在BE段与桌面的动摩擦因数为μ,匀质绳与桌面的摩擦可忽略。初始时刻用手按住木块使其停在A处,绳处于绷紧状态,AB=BC=CD=DE=L,放手后,木块最终停在C处。桌面距地面高度大于6L。

(1)求木块刚滑至B点时的速度v和μ的值?
(2)若木块BE段与桌面的动摩擦因数变为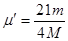 ,则木块最终停在何处?
,则木块最终停在何处?
(3)是否存在一个μ值,能使木块从A处放手后,最终停在E处,且不再运动?若能,求出该μ值;若不能,简要说明理由。

(1)求木块刚滑至B点时的速度v和μ的值?
(2)若木块BE段与桌面的动摩擦因数变为
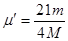 ,则木块最终停在何处?
,则木块最终停在何处?(3)是否存在一个μ值,能使木块从A处放手后,最终停在E处,且不再运动?若能,求出该μ值;若不能,简要说明理由。
(1)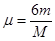 (2)木块将从C点再滑动L最终停在D处(3)见解析
(2)木块将从C点再滑动L最终停在D处(3)见解析
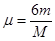 (2)木块将从C点再滑动L最终停在D处(3)见解析
(2)木块将从C点再滑动L最终停在D处(3)见解析(1)木块从A处释放后滑至B点的过程中,由机械能守恒得
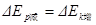
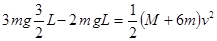 ①
①
则木块刚滑至B点时的速度 ②
②
木块从A处滑至C点的过程中,由能量关系得
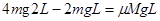 ③
③
由③式得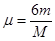 ④
④
(2)若 ,设木块能从B点再向右滑动x最终停止,由能量关系得
,设木块能从B点再向右滑动x最终停止,由能量关系得
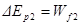 即
即
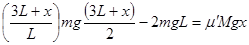 ⑤
⑤
将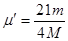 代入⑤式并整理得
代入⑤式并整理得 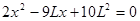
解得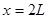 (
(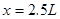 不合题意舍去)
不合题意舍去)
即木块将从C点再滑动L最终停在D处。
(3)不存在符合要求的μ值,即不可能使木块从A处放手后最终停在E处且不再运动。
这是由于当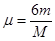 时,若木块能滑至E点,恰好有
时,若木块能滑至E点,恰好有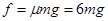 ,此时绳全部悬于桌边外,对木块的拉力恰好也为
,此时绳全部悬于桌边外,对木块的拉力恰好也为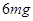 ,而从②式的结果知,要使木块继续向E点滑行,必须再减小μ值,因而木块尚未滑至E点时,木块所受滑动摩擦力已与悬绳拉力相等,此时,再向E点滑行时,悬绳对木块拉力将大于木块受到的滑动摩擦力而使合力向右,木块又重新获得加速度,因此不可能保持静止状态。
,而从②式的结果知,要使木块继续向E点滑行,必须再减小μ值,因而木块尚未滑至E点时,木块所受滑动摩擦力已与悬绳拉力相等,此时,再向E点滑行时,悬绳对木块拉力将大于木块受到的滑动摩擦力而使合力向右,木块又重新获得加速度,因此不可能保持静止状态。
木块从A处释放后滑至B点的过程中,系统机械能守恒,首先规定零势面,找到初状态和末状态,由机械能守恒定律列公式(系统重力势能的减小量等于动能增加量)求解,若 ,设木块能从B点再向右滑动x最终停止,由能量关系可知重力势能的减小量等于克服阻力做功,向右滑动x距离,右端质量下降x,设末状态最低点为零势面计算出高度差可求得重力势能减小量,再由功能关系列式求解,最后讨论即可
,设木块能从B点再向右滑动x最终停止,由能量关系可知重力势能的减小量等于克服阻力做功,向右滑动x距离,右端质量下降x,设末状态最低点为零势面计算出高度差可求得重力势能减小量,再由功能关系列式求解,最后讨论即可
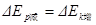
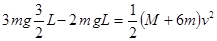 ①
① 则木块刚滑至B点时的速度
 ②
② 木块从A处滑至C点的过程中,由能量关系得
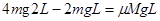 ③
③ 由③式得
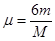 ④
④ (2)若
 ,设木块能从B点再向右滑动x最终停止,由能量关系得
,设木块能从B点再向右滑动x最终停止,由能量关系得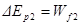 即
即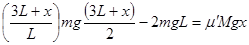 ⑤
⑤ 将
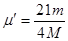 代入⑤式并整理得
代入⑤式并整理得 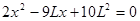
解得
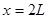 (
(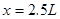 不合题意舍去)
不合题意舍去)即木块将从C点再滑动L最终停在D处。
(3)不存在符合要求的μ值,即不可能使木块从A处放手后最终停在E处且不再运动。
这是由于当
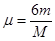 时,若木块能滑至E点,恰好有
时,若木块能滑至E点,恰好有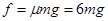 ,此时绳全部悬于桌边外,对木块的拉力恰好也为
,此时绳全部悬于桌边外,对木块的拉力恰好也为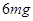 ,而从②式的结果知,要使木块继续向E点滑行,必须再减小μ值,因而木块尚未滑至E点时,木块所受滑动摩擦力已与悬绳拉力相等,此时,再向E点滑行时,悬绳对木块拉力将大于木块受到的滑动摩擦力而使合力向右,木块又重新获得加速度,因此不可能保持静止状态。
,而从②式的结果知,要使木块继续向E点滑行,必须再减小μ值,因而木块尚未滑至E点时,木块所受滑动摩擦力已与悬绳拉力相等,此时,再向E点滑行时,悬绳对木块拉力将大于木块受到的滑动摩擦力而使合力向右,木块又重新获得加速度,因此不可能保持静止状态。 木块从A处释放后滑至B点的过程中,系统机械能守恒,首先规定零势面,找到初状态和末状态,由机械能守恒定律列公式(系统重力势能的减小量等于动能增加量)求解,若
 ,设木块能从B点再向右滑动x最终停止,由能量关系可知重力势能的减小量等于克服阻力做功,向右滑动x距离,右端质量下降x,设末状态最低点为零势面计算出高度差可求得重力势能减小量,再由功能关系列式求解,最后讨论即可
,设木块能从B点再向右滑动x最终停止,由能量关系可知重力势能的减小量等于克服阻力做功,向右滑动x距离,右端质量下降x,设末状态最低点为零势面计算出高度差可求得重力势能减小量,再由功能关系列式求解,最后讨论即可
练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
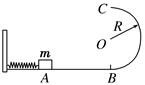
 ,仍要使物体恰能完成BC导轨上的圆周运动,则弹簧开始时的弹性势能至少为多少。
,仍要使物体恰能完成BC导轨上的圆周运动,则弹簧开始时的弹性势能至少为多少。