题目内容
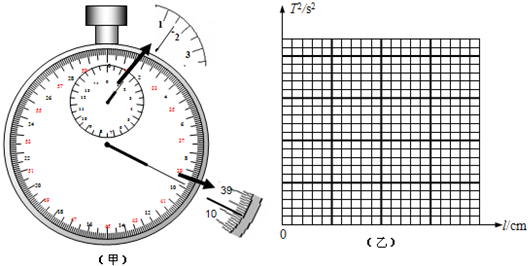
(1)某同学在做“利用单摆测重力加速度”实验中,先测得摆线长为97.50cm,摆球直径为2.00cm,然后用秒表记录了单摆振动50次所用的时间(如图甲),则该摆摆长为
(2)为提高实验精度,该同学在实验中改变摆长l并测出相应的周期T,得出一组对应的l与T的数据如下表所示.
请你帮助该同学以l为横坐标,T 2为纵坐标将所得数据在图乙所示的坐标系中作出图线,并根据图线求得重力加速度g=
98.50
98.50
cm,秒表所示读数为99.8
99.8
s.
(2)为提高实验精度,该同学在实验中改变摆长l并测出相应的周期T,得出一组对应的l与T的数据如下表所示.
| l/cm | 50.0 | 60.0 | 70.0 | 80.0 | 90.0 | 100.0 |
| T/s | 2.02 | 2.51 | 2.83 | 3.18 | 3.64 | 4.05 |
9.86
9.86
m/s2 (取3位有效数字).分析:(1)单摆摆长等于摆线的长度与摆球半径之和;秒表中间的小表盘是分针表盘,
外边的大表盘是秒针表盘,分针示数与秒针示数之和是秒表的示数.
(2)应用描点法作图,根据作出的T2-l图象求出图象的斜率,然后根据单摆周期公式求出重力加速度.
外边的大表盘是秒针表盘,分针示数与秒针示数之和是秒表的示数.
(2)应用描点法作图,根据作出的T2-l图象求出图象的斜率,然后根据单摆周期公式求出重力加速度.
解答: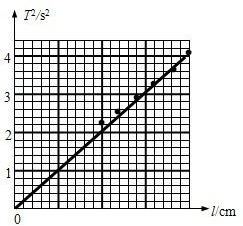 解:(1)单摆摆长等于摆线的长度与摆球半径之和,
解:(1)单摆摆长等于摆线的长度与摆球半径之和,
单摆的摆长L=l+
=97.50cm+
=98.50cm;
由图(甲)所示秒表可知,分针示数是1min=60s,
秒针示数39.8s,秒表示数60s+39.8s=99.8s;
(2)根据表中实验数据,应用描点法作图,T2-l图象如下图所示;由单摆周期公式T=2π
可得,T2=
L,
由此可知T2与L成正比,因此T2-L图象斜率k=
,由图象可知,图象斜率k=4s2/m,则重力加速度g=
=
m/s2≈9.86m/s2;
故答案为:(1)98.50;99.8;(2)图象如下图所示;9.86.
 解:(1)单摆摆长等于摆线的长度与摆球半径之和,
解:(1)单摆摆长等于摆线的长度与摆球半径之和,单摆的摆长L=l+
| d |
| 2 |
| 2.00cm |
| 2 |
由图(甲)所示秒表可知,分针示数是1min=60s,
秒针示数39.8s,秒表示数60s+39.8s=99.8s;
(2)根据表中实验数据,应用描点法作图,T2-l图象如下图所示;由单摆周期公式T=2π
|
| 4π2 |
| g |
由此可知T2与L成正比,因此T2-L图象斜率k=
| 4π2 |
| g |
| 4π2 |
| k |
| 4×(3.14)2 |
| 4 |
故答案为:(1)98.50;99.8;(2)图象如下图所示;9.86.
点评:一定要注意单摆摆长是摆线长度与摆球半径之和,摆线的长度不是摆长;本题难度不大,是一道基础题,牢固掌握基础知识、熟练应用单摆周期公式是正确解题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目


 B.
B. C.
C. D.
D.



 B.
B. C.
C. D.
D.

