题目内容
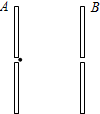 如图所示,A、B为真空中相距为d的一对平行金属板,两板间的电压为U,一带电粒子从A板的小孔进入电场,粒子的初速度可视为零,经电场加速后从B板小孔射出.已知带电粒子的质量为m,所带电荷量为q.带电粒子所受重力不计.求:
如图所示,A、B为真空中相距为d的一对平行金属板,两板间的电压为U,一带电粒子从A板的小孔进入电场,粒子的初速度可视为零,经电场加速后从B板小孔射出.已知带电粒子的质量为m,所带电荷量为q.带电粒子所受重力不计.求:(1)带电粒子从B板射出时的速度大小;
(2)带电粒子在电场中运动的时间.
分析:(1)根据动能定理,即可求解;
(2)根据运动学公式,结合牛顿第二定律与电场强度E=
公式,即可求解.
(2)根据运动学公式,结合牛顿第二定律与电场强度E=
| U |
| d |
解答:解:
(1)设带电粒子从B板射出时的速度为v,根据动能定理:
则有:
mv2=qU
解得,v=
(2)以带电粒子为研究对象,设带电粒子在电场中运动的时间为t,根据运动学公式
设带电粒子在电场中的加速度为a,
由牛顿第二定律,F电=ma
又E=
且F电=qE
解得:a=
由位移公式,d=
at2
解得:t=
=d
答:(1)带电粒子从B板射出时的速度大小v=
;
(2)带电粒子在电场中运动的时间d
.
(1)设带电粒子从B板射出时的速度为v,根据动能定理:
则有:
| 1 |
| 2 |
解得,v=
|
(2)以带电粒子为研究对象,设带电粒子在电场中运动的时间为t,根据运动学公式
设带电粒子在电场中的加速度为a,
由牛顿第二定律,F电=ma
又E=
| U |
| d |
且F电=qE
解得:a=
| qU |
| dm |
由位移公式,d=
| 1 |
| 2 |
解得:t=
|
|
答:(1)带电粒子从B板射出时的速度大小v=
|
(2)带电粒子在电场中运动的时间d
|
点评:考查动能定理、牛顿第二定律及运动学公式的应用,掌握电场强度与电势差的关系,注意正确的运算.

练习册系列答案
相关题目
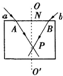
 (2012?广西模拟)如图所示,a、b为两束不同频率的单色光,以45°的入射角射到玻璃砖的上表面,直线OO'与玻璃砖垂直且与其上表面交于N点,入射点A、B到N点的距离相等,进入玻璃砖后两束光相交于图中的P点,则下列说法正确的是( )
(2012?广西模拟)如图所示,a、b为两束不同频率的单色光,以45°的入射角射到玻璃砖的上表面,直线OO'与玻璃砖垂直且与其上表面交于N点,入射点A、B到N点的距离相等,进入玻璃砖后两束光相交于图中的P点,则下列说法正确的是( )