Question

【题目】(12分)如图所示，一个光滑圆筒直立于水平桌面上，圆筒的直径为L，一条长也为L的细绳一端固定在圆筒中心轴线上的O点，另一端拴一质量为m的小球．当小球以速率v绕中心轴线OO′在水平面内做匀速圆周运动时(小球和绳在图中都没有画出，但不会碰到筒底)，求：

(1)当v＝时绳对小球的拉力大小；

(2)当v＝时绳对小球的拉力大小．

Answer 1

【答案】(1)1.09mg　(2)1.15mg

【解析】如图甲所示，

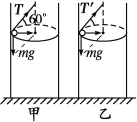
设球刚好挨着圆筒内壁做匀速圆周运动的速度为v0，有mgtan 30°＝m，即v0＝.

(1)当v＝时，v<v0，小球轨迹半径小于圆筒半径，则Tsin α＝m，Tcos α＝mg，由两式可得：

cos α＝0.92，FT＝1.09mg.

(2)当v＝时，v>v0.小球紧贴圆筒内壁做匀速圆周运动，如图乙所示，受筒壁弹力N，由T′cos 30°＝mg，得：T′＝1.15mg.