题目内容
在直角坐标系的第Ⅱ象限和第Ⅳ象限中的直角三角形区域内,分布着磁感应强度均为B的匀强磁场,方向分别垂直纸面向外和向里.某一带正电粒子A1,由静止开始经加速电压为U的电场(图中未画出)加速后,从纵坐标为![]() a的M处平行于x轴向右运动,通过第Ⅱ象限的匀强磁场区域后,在坐标原点O处与静止在该点的粒子A2发生了对心正碰,碰后它们结合在一起进入第Ⅳ象限,碰撞前后它们的运动轨迹如图所示.若两个粒子的质量相等且均可视为质点、重力不计、碰撞过程中无电荷量损失.
a的M处平行于x轴向右运动,通过第Ⅱ象限的匀强磁场区域后,在坐标原点O处与静止在该点的粒子A2发生了对心正碰,碰后它们结合在一起进入第Ⅳ象限,碰撞前后它们的运动轨迹如图所示.若两个粒子的质量相等且均可视为质点、重力不计、碰撞过程中无电荷量损失.
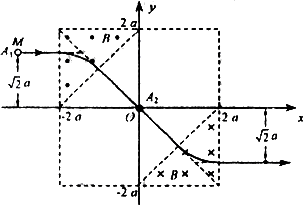
(1)求带电粒子A1的比荷(即q/m):
(2)确定粒子A2碰撞前的带电情况;
(3)求带电粒子A1在两个磁场区域中偏转所用的总时间.
解析:
|
(1)带电粒子Al在电场中被加速,由动能定理有qU= 在磁场中偏转,由牛顿第二定律有qυB=m 联立①②两式得q/m=2U/(B2r2) ③ (1分) 由图可知r= 代人③式解得q/m=U/(B2a2) ④ (2分) (2)由①④两式可得A1在第Ⅱ象限的磁场中的运动速率 v= 在O点A1、A2碰撞后结合在一起.由动量守恒定律有2m 由②⑥式结合粒子运动轨迹的特点有 故有 (3)由函可知粒子A1在两个磁场中分别偏转的弧度为π/4. 而T=2πr/υ ⑧ (1分) tl=T1/8=πr/(4v)=πa2B/(4U) (1分) t2=T2/8=πr/(4 所以它在磁场中运动的总时间t=t1+t2=3πa2B/(4U) (1分) |

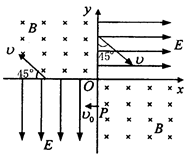
 如图所示,在直角坐标系的第Ⅰ象限和第Ⅲ象限存在着电场强度均为E的匀强电场,其中第Ⅰ象限电场沿x轴正方向,第Ⅲ象限电场沿y轴负方向.在第Ⅱ象限和第Ⅳ象限存在着磁感应强度均为B的匀强磁场,磁场方向均垂直纸面向里.有一个电子从y轴的P点以垂直于y轴的初速度v0进入第Ⅲ象限,第一次到达x轴上时速度方向与x轴负方向夹角为45°,第一次进入第Ⅰ象限时,与y轴夹角也是45°,经过一段时间电子又回到了P点,进行周期性运动.已知电子的电荷量为e,质量为m,不考虑重力和空气阻力.求:
如图所示,在直角坐标系的第Ⅰ象限和第Ⅲ象限存在着电场强度均为E的匀强电场,其中第Ⅰ象限电场沿x轴正方向,第Ⅲ象限电场沿y轴负方向.在第Ⅱ象限和第Ⅳ象限存在着磁感应强度均为B的匀强磁场,磁场方向均垂直纸面向里.有一个电子从y轴的P点以垂直于y轴的初速度v0进入第Ⅲ象限,第一次到达x轴上时速度方向与x轴负方向夹角为45°,第一次进入第Ⅰ象限时,与y轴夹角也是45°,经过一段时间电子又回到了P点,进行周期性运动.已知电子的电荷量为e,质量为m,不考虑重力和空气阻力.求: