题目内容
【题目】如图所示，水平传送带以v=2m/s的速率沿逆时针方向转动，在其左端与一竖直固定的光滑轨道平滑相接，右端与一半径R=0.4m的光滑半圆轨道相切，一质量m=2kg的物块（可视为质点）从光滑轨道上的某点由静止开始下滑，通过水平传送带后从半圆轨道的最高点水平抛出，并恰好落在传送带的最左端，已知物块通过半圆轨道最高点时受到的弹力F=60N，物块与传送带间的动摩擦因数μ=0.25，取重力加速度g=10m/s2，求：（计算结果可以保留根号）
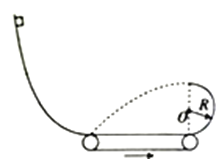
（1）物块作平抛运动的初速度v0；
（2）物块开始下滑时距水平传送带的高度H；
（3）电动机由于物块通过传送带而多消耗的电能E．
【答案】见解析。
【解析】
试题分析：（1）物块在最高点
·
·········（ 2分
代入数据得：v0=4m/s 1分
（2）物块离开最高点后做平抛运动，由：
···········（ 2分
得运动的时间：
0.4s 1分
物块沿水平方向平抛有：
L=v0t=4×0.4=1.6m···········（ 1分
则，传送带的长度是1.6m 。由动能定理得：
·
··········（ 2分
代入数据得：H=2m 1分
（3）物块到达传送带的左端的速度
··········（ 2分
得：
m/s
物块在传送带上的加速度a：
·········（ 1分
a=
m/
物块经过传送带的时间t′，则：
········· 1分
该时间内传送带运动的距离：L′=v1t′········· 1分
传送带克服摩擦力做的功：W=fL′=μmgL′ ········· 1分
即：E=W ········· 1分
联立以上各式，代入数据得：E=8（
）J≈3J 1分
练习册系列答案
相关题目
