Question

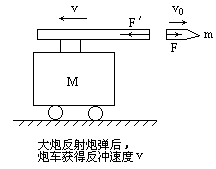
如下图所示，炮身和炮车的总质量为M(不包括炮弹质量)，现以相对于地的水平速度v₀发射一颗质量为m的炮弹．设从开始发射到炮弹离开炮身的时间为Δt．试用动量定理和牛顿第三定律说明发射过程系统动量守恒．

Answer 1

答案：
解析：

我们先考察炮弹，发射过程中它的动量变化为mv0，由守恒定理，炮弹的动量变化应等于爆炸力F对炮弹的冲量FΔt；再考察炮身和炮车，由于它受到反作用力的冲量Δt的作用，动量也要发生变化，结果获得了一个反冲速度v，但由于FΔt和Δt的大小相等，方向相反，因此，炮弹的动量变化与炮身和炮车的动量变化应是大小相等，方向相反的． 　　若把炮弹、炮身和炮车看成一个系统，则系统的总动量守恒．其实，因为系统所受的合外力为零，则合外力的冲量为零，而系统的内力对系统的总冲量总是为零的，所以，没有内在和外在的原因来改变系统的动量，系统的总动量自然是守恒的．其动量守恒方程可写为：mv0＝Mv．