题目内容
16．
如图所示为用绞车拖物块的示意图，拴接物块的细线被缠绕在轮轴上，轮轴逆时针转动从而拖动物块．已知轮轴的半径R=0.5m，细线始终保持水平，被拖动物块质量m=1kg，与地面间的动摩擦因数μ=0.5，轮轴的角速度随时间变化的关系是ω=2trad/s，g=10m/s2．以下判断正确的是（ ）| A． | 物块做匀速直线运动 | |
| B． | 物块做匀加速直线运动，加速度大小是2m/s2? | |
| C． | 绳对物块的拉力是5N | |
| D． | 绳对物块的拉力是6N |
分析 由物块速度v=ωR=at，可得物块运动的加速度，结合牛顿第二定律即对物块的受力分析可求解绳子拉力．
解答 解：A、物块的速度：v=ωR=2t×0.5=t，随时间增加，物块的速度不断增大，物块做加速直线运动，故A错误；
B、物块的速度：v=tm/s，由速度公式：v=at可知，物块做初速度为零的匀加速直线运动，加速度：a=1m/s2，故B错误；
C、对物块，由牛顿第二定律得：F-μmg=ma，解得：F=μmg+ma=0.5×1×10+1×1=6N，故C错误，D正确；
故选：D．
点评 本题关键根据绞车的线速度等于物块运动速度从而求解物块的加速度，根据牛顿第二定律求解．
练习册系列答案
阅读快车系列答案
相关题目
6．一辆质量为1kg的遥控电动玩具小汽车从静止开始先做匀加速直线运动，再做匀速直线运动，最后做匀减速直线运动，直到停止．玩具小汽车在运动过程中所受的阻力恒为车重的0.6倍，g=10m/s2，下表记录了不同时刻玩具小汽车的速度：
下列说法正确的是（ ）
| 时刻/s | 1.0 | 2.0 | 3.0 | 5.0 | 7.0 | 9.5 | 10.5 |
| 速度/m•s-1 | 3 | 6 | 9 | 12 | 12 | 9 | 3 |
| A． | 玩具小汽车做匀速直线运动的速度是12m/s，时间是2s | |
| B． | 玩具小汽车在加速阶段和减速阶段的平均速度相同 | |
| C． | 玩具小汽车在减速阶段运动的位移是12m | |
| D． | 玩具小汽车在加速阶段的牵引力是8N |
如图所示，足够长的木板静止在粗糙的水平地面上，木板的质量M=2kg，与地面间的动摩擦因数μ1=0.1；在木板的左端放置一个质量m=2kg的小铅块（视为质点），小铅块与木板间的动摩擦因数μ2=0.3．现给铅块一向右的初速度v0=4m/s，使其在木板上滑行，木板获得的最大速度v=1m/s，g取10m/s2，木板达到最大速度时，求：
如图所示，光滑的水平面上放置一长木板，长木板处于静止状态，长木板的质量是1kg，在长木板的左端放一个小滑块（可视为质点），小滑块的质量也是1kg，小滑块与长木板之间的动摩擦因数为0.2，某时刻对长木板施加一水平向左的恒力，大小为6.0N，小滑块开始在长木板上滑动，经过1.0s的时间，撤去水平恒力，小滑块在滑动过程中始终没有从长木板上掉下去（g取10m/s2），求：
11．如图所示，一个正电子沿逆时针方向做匀速圆周运动，下列判断正确的是（ ）
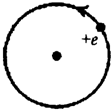
| A． | 正电子运动时不产生磁场 | |
| B． | 正电子运动时只在圆周内产生磁场 | |
| C． | 正电子运动时产生磁场，圆心处的磁场方向垂直纸面向外 | |
| D． | 正电子运动时产生磁场，圆心处的磁场方向垂直纸面向里 |
一个滑雪者，质量m=70kg，从静止开始沿山坡匀加速滑下，已知滑雪者运动的加速度大小a=4m/s2，山坡可看成足够长的斜面．
如图所示，在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B，它们的质量相等，均为m，弹簧的劲度系数为k，C为一固定挡板．系统处于静止状态．现开始用沿斜面方向的力F（F未知）拉物块A使之向上做加速度为a的匀加速运动，当物块B刚要离开C时，沿斜面方向的力为F（F未知）保持此时的值变为恒力，且此时弹簧与物块A连接处断裂，物块A在恒力作用下继续沿斜面向上运动．重力加速度为g，求：
6．
古巴运动员哈维尔•索托马约尔，在西班牙萨拉曼卡举行的国际田径赛上，跳出了2.43m的好成绩，刷新了男子跳高的世界纪录．若不计空气阻力，以下说法正确的是（ ）
古巴运动员哈维尔•索托马约尔，在西班牙萨拉曼卡举行的国际田径赛上，跳出了2.43m的好成绩，刷新了男子跳高的世界纪录．若不计空气阻力，以下说法正确的是（ ）| A． | 马约尔达到2.43 m高度时，他的速度为0 | |
| B． | 起跳时地面对他的支持力大于他对地面的压力 | |
| C． | 起跳时地面对他的支持力与他的重力大小相等 | |
| D． | 起跳时地面对他的支持力大于他的重力 |