题目内容
 (2010?江西二模)如图所示,质量为m,带电量为+q的微粒在0点以初速度v0与水平方向成θ 角射出,微粒在运动中受阻力大小恒定为f.
(2010?江西二模)如图所示,质量为m,带电量为+q的微粒在0点以初速度v0与水平方向成θ 角射出,微粒在运动中受阻力大小恒定为f.①如果在某方向加上一定大小的匀强电场后,能保证微粒仍沿u方向做直线运动,试求所加匀强电场的最小值?
②若加上大小一定,方向水平向左的匀强电场,仍能保证微粒沿vo方向做直线运动,并经过一段时间后又返回o点,求微粒回到o点时的速率?
分析:(1)保证微粒仍沿vo方向做直线运动,电场力方向必须垂直于vo方向斜向上时,电场力有最小值,则场强有最小值,根据垂直于vo方向合力为零,求出电场强度的最小值.
(2)若加上大小一定,方向水平向左的匀强电场,仍能保证微粒沿vo方向做直线运动,微粒所受的合力方向与vo方向相反,根据动能定理分别研究微粒从O点到速度为零的过程和整体过程,求出微粒回到O点时的速率.
(2)若加上大小一定,方向水平向左的匀强电场,仍能保证微粒沿vo方向做直线运动,微粒所受的合力方向与vo方向相反,根据动能定理分别研究微粒从O点到速度为零的过程和整体过程,求出微粒回到O点时的速率.
解答:解:(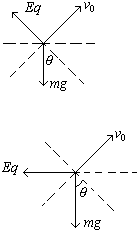 1)微粒受力如图所示,要保证微粒沿vo方向直线运动必须使垂直于vo方向斜上方加匀强电场,E有最小值,且Eq=mgcosθ,E=
1)微粒受力如图所示,要保证微粒沿vo方向直线运动必须使垂直于vo方向斜上方加匀强电场,E有最小值,且Eq=mgcosθ,E=
.
(2)如图所示,为使垂直于v0方向合力为零,Eqsinθ=mgcosθ.设微粒最大位移为S,由动能定理
-(mgsinθ+qEcosθ+f)S=0-
m
粒子由O点射出再回到O点整个过程,由动能定理
-2fS=
mv2-
m
.
解上述方程得
v=
v0.
答:
①如果在某方向加上一定大小的匀强电场后,能保证微粒仍沿u方向做直线运动,所加匀强电场的最小值为E=
.
②微粒回到O点时的速率为v=
v0.
 1)微粒受力如图所示,要保证微粒沿vo方向直线运动必须使垂直于vo方向斜上方加匀强电场,E有最小值,且Eq=mgcosθ,E=
1)微粒受力如图所示,要保证微粒沿vo方向直线运动必须使垂直于vo方向斜上方加匀强电场,E有最小值,且Eq=mgcosθ,E=| mgcosθ |
| q |
(2)如图所示,为使垂直于v0方向合力为零,Eqsinθ=mgcosθ.设微粒最大位移为S,由动能定理
-(mgsinθ+qEcosθ+f)S=0-
| 1 |
| 2 |
| v | 2 0 |
粒子由O点射出再回到O点整个过程,由动能定理
-2fS=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
解上述方程得
v=
|
答:
①如果在某方向加上一定大小的匀强电场后,能保证微粒仍沿u方向做直线运动,所加匀强电场的最小值为E=
| mgcosθ |
| q |
②微粒回到O点时的速率为v=
|
点评:本题要根据微粒做直线运动的条件:合力方向与速度方向在同一直线上.对于有往复运动的问题,运用动能定理可分段研究,也可以全过程研究.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

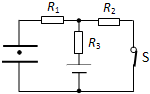 (2010?江西二模)电源和一个水平放置的平行板电容器、三个电阻组成如图所示的电路.当开关S闭合后,电容器中有一个带电液滴正好处于静止状态.现将开关S断开,则以下判断正确的是( )
(2010?江西二模)电源和一个水平放置的平行板电容器、三个电阻组成如图所示的电路.当开关S闭合后,电容器中有一个带电液滴正好处于静止状态.现将开关S断开,则以下判断正确的是( ) (2010?江西二模)如图所示,用三块完全相同的平板玻璃组成一等边三角形,一束单色光由AB面入射,由AC面射出,则以下说法正确的是( )
(2010?江西二模)如图所示,用三块完全相同的平板玻璃组成一等边三角形,一束单色光由AB面入射,由AC面射出,则以下说法正确的是( ) (2010?江西二模)如图所示的电路可用于测量电源电动势E,内阻r0和
(2010?江西二模)如图所示的电路可用于测量电源电动势E,内阻r0和 表的内阻RV,图中
表的内阻RV,图中 表的内阻不能忽略,大小未知.R是一个限流电阻,阻值也未知,3个开关K1,K2,K3都处于断开状态.
表的内阻不能忽略,大小未知.R是一个限流电阻,阻值也未知,3个开关K1,K2,K3都处于断开状态.