Question

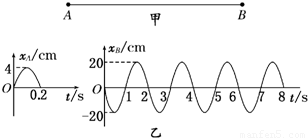
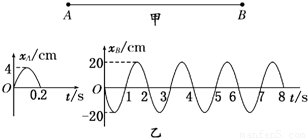
如图甲所示，在某介质中波源A、B相距d=20m，t=0时两者开始上下振动，A只振动了半个周期，B连续振动，所形成的波的传播速度都为v=1.0m/s，开始阶段两波源的振动图象如图乙所示．
（1）定性画出t=14.3s时A波所达位置一定区域内的实际波形；
（2）求时间t=16s内从A发出的半波前进过程中所遇到的波峰个数．

Answer 1

分析：（1）运用波形的平移法分别画出两波在t=14.3s时的波形，再波的叠加原理，画出叠加区域的波形．
（2）波在t时间内传播的距离为x=vt，根据几何关系求得16 s内两列波相对运动的长度，结合两波的长度，求解．

解答：解：（1）分别画出A波在14.3 s时的波形图，B波在14.3 s 时的波形图，两列波叠加可得到波形图如图所示，
（2）16 s内两列波相对运动的长度为
△l=l_A+l_B-d=2vt-d=12 m，
A波宽度为a=

λA

2

=v

TA

2

=0.2 m．
B波波长为λ_B=vT_B=2 m
可知A波经过了6个波峰．
答：（1）图见解析　（2）时间t=16s内从A发出的半波前进过程中所遇到的6个波峰．

点评：本题考查对波的叠加原理的理解和应用能力，要注意波的叠加也遵守矢量的运算法则．